Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 68

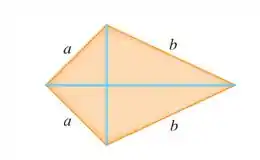
A moldura para uma pipa é feita com seis pedaços de madeira. Os quatro pedaços externos foram cortados com os comprimentos indicados na figura. Para maximizar a área da pipa, de que tamanho devem ser os pedaços diagonais?

Passo 1

Fala aí! tudo certinho?

Nesse problema temos uma pipa conforma descrito na imagem do problema e nosso objetivo é determinar os valores das diagonais em azul que maximizam a area da pipa.

Com as informações dadas no enunciado, podemos esboçar o seguinte desenho:

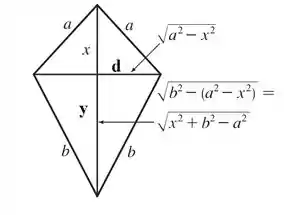
A partir daí calculamos a area total da pipa criando uma função área A .

Para maximizar essa função, derivamos e igualamos a 0 para obter seus pontos críticos.

Sacou? Bora começar!

Passo 2

Para calcular a área máxima precisamos das áreas dos triângulos retângulos menores, fazendo A = b h 2 , então isolamos as medidas da figura por meio de Pitágoras:

A partir do triangulo menor, temos

a 2 = x 2 + d 2 → d = a 2 - x 2

E do triangulo maior...

b 2 = d 2 + y 2

Substituindo d nessa equação

b 2 = ( a 2 - x 2 ) + y ²

y = x 2 + b 2 - a 2

Show?

Calculando a área total da pipa, temos

A = 2 a 2 - x 2 x 2 + 2 a 2 - x 2 x 2 + b 2 - a 2 2

A = a 2 - x 2 x + x 2 + b 2 - a 2   ,   0 ≤ x ≤ a

x varia entre 0 e a para que não dê números negativos dentro das raízes.

Tranquilo até aqui?

Passo 3

Maximizando A , derivamos e igualamos a 0 ...

Pela regra da cadeia e do produto...

A ' x = a 2 - x 2 1 + x x 2 + b 2 - a 2 + x + x 2 + b 2 - a 2 - x a 2 - x 2 = 0

x a 2 - x 2 x + x 2 + b 2 - a 2 = a 2 - x 2 x + x 2 + b 2 - a 2 x 2 + b 2 - a 2

Temos o fator x + x 2 + b 2 - a 2   multiplicando nos dois lados, então podemos cancelá-los:

x a 2 - x 2 = a 2 - x 2 x 2 + b 2 - a 2

x x 2 + b 2 - a 2 = a 2 - x 2

Elevando os dois lados ao quadrado para simplificar a raiz...

x 2 x 2 + b 2 - a 2 = a 4 - 2 a 2 x 2 + x 4

x 2 b 2 - a 2 = a 4 - 2 a 2 x 2

x 2 b 2 - a 2 x 2 + 2 a 2 x 2 = a 4

Vamos isolar x em um lado da igualdade...

x 2 b 2 + a 2 x 2 = a 4

x 2 b 2 + a 2 = a 4

x 2 = a 4 a 2 + b 2

x = a 2 a 2 + b 2

Show?

Passo 4

Encontrado o valor de x que maximiza a área, podemos substituir nos tamanhos diagonais desejados.

Essas substituições são monstruosas então faça com calma para não se perder!

Para o pedaço horizontal:

2 d = 2 a 2 - x 2

2 d = 2 a 2 - a 4 a 2 + b 2

Vamos simplificar a raiz deixando tudo no mesmo denominador

2 d = 2 a 2 a 2 + b 2 a 2 + b 2 - a 4 a 2 + b 2

2 d = 2 a 2 b 2 a 2 + b 2

2 d = 2 a b a 2 + b 2

Agora para o pedaço vertical:

x + y = x + x 2 + b 2 - a 2

x + y = a 4 a 2 + b 2 + a 4 a 2 + b 2 + b 2 - a 2

Vamos simplificar a raiz deixando tudo no mesmo denominador...

x + y = a 4 a 2 + b 2 + a 4 a 2 + b 2 + b 2 a 2 + b 2 a 2 + b 2 - a 2 a 2 + b 2 a 2 + b 2

x + y = a 4 a 2 + b 2 + a 4 + a 2 b 2 + b 4 - a 4 - a 2 b 2 a 2 + b 2

Perceba que podemos simplificar o numerador da raiz

x + y = a 4 a 2 + b 2 + a 4 + b 4 a 2 + b 2 = a 2 + b 2 a 2 + b 2

x + y = a 2 + b 2

É isso! O que achou? Responde Aí!

Resposta

Pedaço horizontal: 2 a b a 2 + b 2

Pedaço vertical: a 2 + b 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o seguinte problema: encontre dois números cuja soma seja 23 e cujo produto seja máximo.Faça uma tabela de valores, como mostrada a seguir, tal que a soma dos números nas duas primeiras colu
Dentre as infinitas restas tangentes à curva y = - sen ⁡ x que passam pela origem, existe uma que tem a maior inclinação. Use o método de Newton para encontrar a inclinação daquela reta com precisão d
Use o método de Newton para encontrar as coordenadas, com precisão de seis casas decimais, do ponto na parábola y = x - 1 2 que esteja mais próximo da origem.
Um pedaço de fio com 10m de comprimento é cortado em duas partes. Uma parte é dobrada no formato de um quadrado, ao passo que a outra é dobrada na forma de um triângulo equilátero. Como deve ser corta
Uma janela normanda tem a forma de um retângulo tendo em cima um semicírculo. (O diâmetro do semicírculo é igual à largura do retângulo). Se o perímetro da janela for 10m , encontre as dimensões da ja