Nos Exercícios 33 e 34, uma partícula está se movendo ao longo de uma reta horizontal, de acordo com a equação dada, onde s cm é a distância orientada da partícula até a origem, v cm/s é a velocidade da partícula e a cm/s² é a aceleração da partícula no instante t s. Ache v e a em termos de t. Faça uma tabela similar à Tabela 1 que dê uma descrição da posição e movimento da partícula. Inclua na tabela os intervalos de tempo, onde a partícula está se movendo para a direita e para a esquerda, onde a velocidade é crescente e decrescente, quando a velocidade escalar é crescente e decrescente, e a posição da partícula com relação à origem nesses intervalos. Mostre o comportamento do movimento numa figura similar à Figura 1.
33.
Passo 1
Para achar v e a em termos de t como o enunciado pede, basta derivar uma vez para encontrar v e depois derivar mais uma vez para achar a.
Para saber se a partícula está à direita ou a esquerda da origem basta analisar o sinal de s, nos intervalos de tempo.

Para saber se a partícula se move para direita ou esquerda, basta avaliar o sinal de v, nos intervalos de tempo.

Para saber se a velocidade da partícula é decrescente o crescente basta avaliar o sinal de a, nos intervalos de tempo.

Para saber se a velocidade escalar da partícula é decrescente o crescente basta avaliar o sinal de a e v, nos intervalos de tempo.
![]()
Passo 2
Vamos derivar a função em função de t para encontrar :
Agora derivando em função de t para encontrar :
Passo 3
Vamos agora analisar para quais valores de t essas três quantidades se anulam.
1º -
Logo temos que para equação ser verdadeira:
Agora analisamos para que valores de t a seguinte equação é verdadeira:
Assim se anula para:
Passo 4
2º -
Assim se anula para:
Passo 5
3º -
Assim se anula para:
Passo 6
Agora vamos montar a tabela pedida no enunciado.
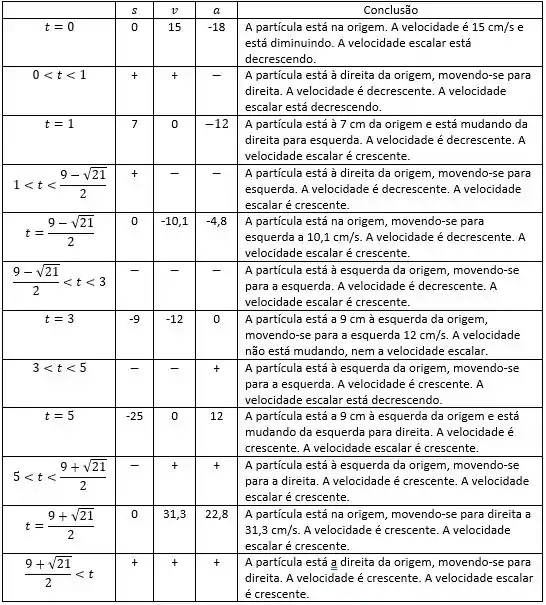
Passo 7
Abaixo está a figura que representa o comportamento do movimento.
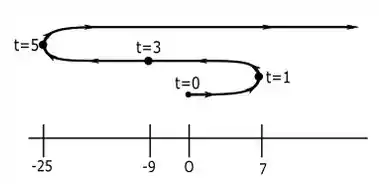
Resposta
Ei, a resposta está no passo a passo :)