Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.6 - Ex. 74
Para o limite
Ilustre a Definição 9 encontrando um valor de N que corresponde a
Passo 1
Olá, meu querido estudante. Pronto para mais uma resolução?
Aqui a gente quer utilizar a Definição 9, para encontrar um valor de que corresponda a . Mas quem é e ? Para responder essas perguntas deveremos dar uma olhada no que diz a definição 9.
Bom pessoal, vamos ver o que diz a Definição 9:
Seja uma função definida em um intervalo Então:
Significa que para todo número positivo existe um número positivo correspondente tal qual:
Então nós vamos fazer o caminho contrário. Iremos encontrar qual o valor de faz com nossa função seja:
Para essa atividade específica, nos é pedido para utilizarmos um software matemático, vamos utilizar o GeoGebra, ele irá nos ajudar a encontrar um valor com maior exatidão.
Passo 2
Temos a seguinte relação:
Plotando o gráfico da função .
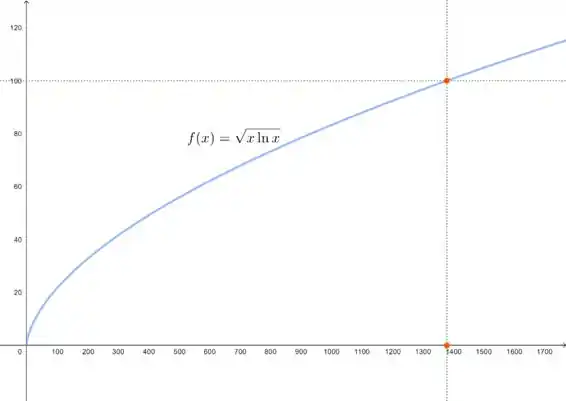
Quando temos. Então, podemos estabelecer um numero N imediatamente maior:
De modo que, para qualquer:
Então: