Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.7 - Ex. 25
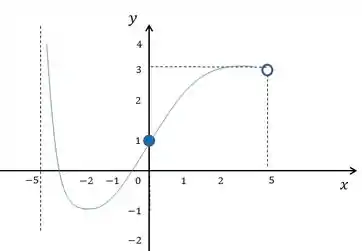
Esboce o gráfico de uma função que é continua no domínio e onde e
Passo 1
Eaee, belezinha?? Bom... queremos esboçar a função no intervalo .
O problema é que não nos foi dada a função e sim o seguinte:
- O valor da função para :
- O valor da derivada em :
- O valor da derivada em :
- O limite lateral direito de tendendo a , ou seja, tendendo pelos valores maiores:
- E o limite lateral esquerdo de tendendo a , ou seja, tendendo pelos valores menores:
Dessa forma, para esboçarmos o gráfico, temos que entender o que cada expressão dessa significa.
Agora bora lá!! 😉
Passo 2
Vamos primeiro analisar os pontos que nos foram dados:
Para temos que quando , .
Já para podemos verificar que trata-se que a inclinação da tangente da curva no ponto zero é .
Em seguida, para , percebemos que a tangente da curva é horizontal.
Passo 3
Agora vamos analisar os limites.
Primeiro vamos dar uma olhada em
Note que quanto mais se aproxima de pela direita, mais a função tende ao infinito positivo.
Assim, podemos concluir que trata-se de uma assíntota vertical em , com a curva subindo até infinito.
Passo 4
Agora vamos analisar:
Podemos perceber que quando tende a pela esquerda, a função tende a (intervalo aberto).
Passo 5
Juntando todas essas informações, podemos esboçar o gráfico:
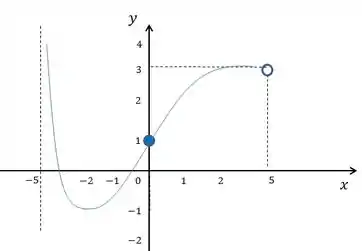
Resposta
