Mostre que a equação de uma cônica que tem eixo principal ao longo do semi-eixo e de sua extensão, um foco na origem e cuja diretriz correspondente está acima do foco é

Devemos lembrar que é a excentricidade e vamos considerar , pois, se , temos uma parábola tendo como ponto fixo seu foco e como reta fixa sua diretriz.

Quando a diretriz está à esquerda do foco, nós temos a equação e a representação abaixo:

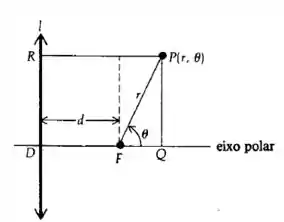
Para obter a equação de quando a diretriz está acima do foco, basta fazer uma rotação da cônica em , ou seja, ao invés de , usar . Perceba que rotacionar por equivale a rotacionar por e depois por . Rotacionando por nós conseguimos a equação de quando a diretriz está à direita e depois rotacionando por mais conseguimos uma cônica com diretriz acima do foco.

Sendo assim, ficamos com:

Ou seja,

Como queríamos mostrar.