Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 78

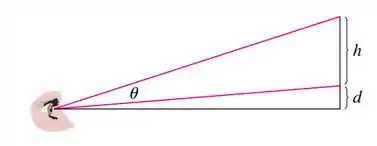
Uma pintura em uma galeria de arte tem altura h e está pendurada de forma que o lado de baixo está a uma distância d   acima do olho de um observador (como na figura). A que distância da parede deve ficar o observador para obter a melhor visão? (Em outras palavras, onde deve ficar o observador de forma a maximizar o ângulo θ subentendido em seu olho pela pintura?)

Passo 1

Fala aí! tudo certinho?

Nesse problema temos uma situação em que um observador está a uma distância x de uma tela e o seu campo de visão consegue captar apenas uma parte h dessa tela restando uma distância d .

A partir daí queremos otimizar essa distância x do observador para que ele consiga observar toda a tela.

Parece complicado?

Para resolver esse problema temos que determinar uma equação que relacione o ângulo θ com a distância x e os valores de h e d ...

A partir daí podemos aplicar o que aprendemos para determinar os pontos de máximo e mínimo de uma função... se queremos minimizar a distância x , temos que derivar θ em função de x e igualar a 0 para encontrar os pontos críticos.

Sacou? Bora começar!

Passo 2

Primeiro temos que encontrar a equação θ em função de x ... vamos analisar a figura

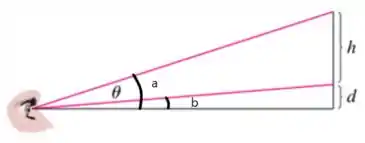
Podemos dizer que θ é dado por

θ = a - b

já o ângulo a pode ser escrito pela regra da tangente

tan ⁡ a = h + d x → a = tan - 1 ⁡ h + d x

Da mesma forma podemos escrever que b é

tan ⁡ b = d x → b = tan - 1 ⁡ d x

Substituindo em θ , temos

θ = tan - 1 ⁡ h + d x - tan - 1 ⁡ d x ,     x > 0

Pronto... encontramos uma equação que relaciona θ e x ...

Tranquilo até aqui?

Passo 3

Agora vamos maximizar θ derivando em relação a x e igualando a 0 ...

d θ d x = d tan - 1 ⁡ h + d x d x - d tan - 1 ⁡ d x d x

Pelo teorema fundamental do cálculo, a derivada de tan - 1 ⁡ x é

d tan - 1 ⁡ x d x = 1 1 + x 2

Aplicando tambem a regra da cadeia, temos

d θ d x = d h + d x d x · d tan - 1 ⁡ u d u - d d x d x · d tan - 1 ⁡ v d v

d θ d x = 1 1 + h + d x 2 - h + d x 2 - 1 1 + d x 2 - d x 2

Igualando a 0 e simplificando...

- h + d x 2 + h + d 2 + d x 2 + d 2 = 0

d x 2 + h + d 2 - h + d x 2 + d 2 x 2 + h + d 2 x 2 + d 2 = 0

h 2 d + h d 2 - h x ² [ x ² ( h + d ) ² ] ( x 2 + d ² ) = 0

Para essa equação ser verdadeira, seu denominador tem que ser igual a 0 , ou seja

h 2 d + h d 2 - h x 2 = 0

Isolando x , temos

h x 2 = h 2 d + h d 2

x 2 = h d + d 2

x = d h + d

Logo, a distância que o observador deve ficar da parede é d h + d .

E aí! o que achou? Responde Aí!

Resposta

x = d h + d

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 40 a 45, uma partícula está se movendo ao longo de uma reta, de acordo com a equação de movimento dada, onde s cm é a distância orientada entre a partícula e a origem no instante t s
Nos exercícios de 40 a 45, uma partícula está se movendo ao longo de uma reta, de acordo com a equação de movimento dada, onde s cm é a distância orientada entre a partícula e a origem no instante t s
Nos Exercícios de 35 a 39, uma partícula está se movendo ao longo de uma reta, de acordo com a equação dada, onde s (m) é a distância orientada entre a posição da partícula e a origem no instante t (s
Nos exercícios de 40 a 45, uma partícula está se movendo ao longo de uma reta, de acordo com a equação de movimento dada, onde s cm é a distância orientada entre a partícula e a origem no instante t s
Nos Exercícios de 35 a 39, uma partícula está se movendo ao longo de uma reta, de acordo com a equação dada, onde s (m) é a distância orientada entre a posição da partícula e a origem no instante t (s