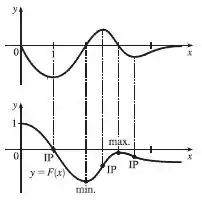
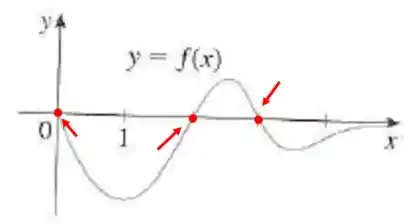
O gráfico de uma função está mostrado na figura. Faça um esboço de uma primitiva de , dado que .
Passo 1
Fala aí, tudo certinho por aí?
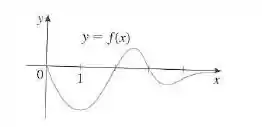
Bom, nesse exercício nos é dado o seguinte gráfico:
E estamos interessados em fazer um esboço de uma primitiva da função representada nesse gráfico.
Para isso, iremos utilizar os conceitos de derivada de decrescimento, crescimento, valores de máximo, valores de mínimo e pontos de inflexão para esboçar uma primitiva de .
E teremos que lembrar que quando:

Olhando para o gráfico dado, podemos analisar o que está acontecendo com a primitiva da nossa função com base, nas informações sobre sua derivada.
Vem que te mostro como.
Passo 2
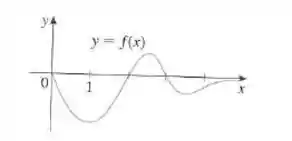
Olhando para o gráfico, podemos ver que existem três pontos de máximo e mínimo.
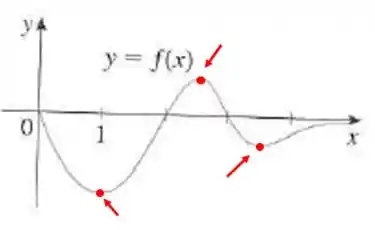
Nesses pontos, deverá haver um ponto de inflexão no gráfico de .
Nos valores em que é negativa, deverá estar decrescendo e nos valores que é positiva, deverá crescer.
Nos valores onde sai do positivo para o negativo, deveremos ter um ponto de máximo e nos valores aonde sai do negativo para o positivo, deveremos ter um ponto de mínimo.
Passo 3
Podemos então gerar o seguinte gráfico
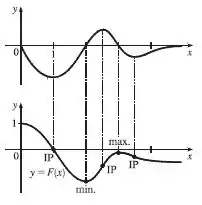
E prontinho.
Resposta