Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.7 - Ex. 18
Uma placa com a forma da região limitada pela parábola x² = 6y e pela reta 2y = 3 é colocado num tanque com agua com o vértice para baixo e a reta na superfície da agua.
Encontre a força decorrente da pressão da agua sobre o lado da placa. (a distância é medida em metros)
Resolva usando F =
Passo 1
Desenhando o problema
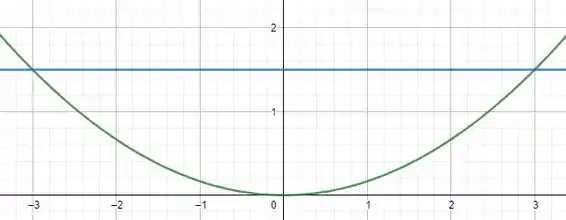
A área dessa região é a integral de (y = 3/2) – (x² = 6y), com x entre [-3,3]
Como Nossa função é par, logo podemos fazer
=
= 2 ( 9/2 – 3³/18)
= 6
Sabendo que
da agua = 10³ kg/m³
g = 10m/s²
Queremos F.
Passo 2
Logo : F = onde é a altura do objeto mergulhado.
F =
Resposta
Exercícios de Livros Relacionados
Uma placa de metal foi encontrada verticalmente imersa em água do mar, que tem uma densidade de 64l b / p é 3 é . As medidas da largura da placa foram tiradas nas profundidades indicadas. Use a Regra
Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. Ent
3. Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann.
Uma placa vertical é submersa (ou parcialmente submersa) em água e tem o formato indicado. Explique como aproximar a força hidrostática contra um lado da placa por uma soma de Riemann. Então expresse
5. Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann.