Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 8.3 - Ex. 7
Uma placa vertical é submersa (ou parcialmente submersa) em água e tem o formato indicado. Explique como aproximar a força hidrostática contra um lado da placa por uma soma de Riemann. Então expresse a força como uma integral e calcule-a.
Passo 1
Vamos começar o exercício esboçando a região e definindo o sistema de coordenadas de maneira com que possamos definir uma área infinitesimal para integração.
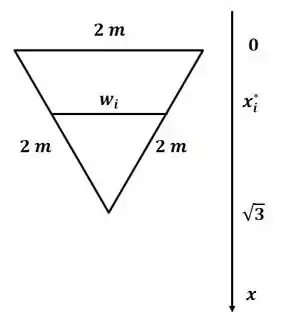
Nesse caso, a largura da placa () varia com o comprimento, então, na i-ésima porção, por semelhança de triângulos, temos:
Dessa forma, a pressão nessa seção infinitesimal será:
Onde é a densidade da água e é a aceleração da gravidade. Dessa forma, a força na área infinitesimal é:
Passo 2
Com isso, a força hidrostática total será aproximada pela soma de Riemann como:
E, com essa informação, podemos calcular a integral como:
Podemos reescrever a integral, retirando as constantes:
Passo 3
Resolvendo a integral obtida no passo 2, temos:
E, com isso o valor da força na placa será: