Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 76
Prove analiticamente que o conjunto de pontos equidistantes de dois pontos dados é a perpendicular pelo ponto médio do segmento que liga os pontos.
Passo 1
Dado um conjunto de pontos, A e B, equidistantes dos pontos dados P1 e P2, precisamos provar que o segmento P1P2 corta AB no seu ponto médio com um ângulo de 90°.
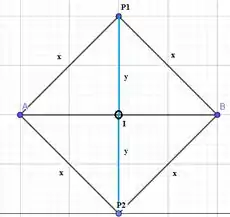
Por ser equidistante: AP1 = BP1 = BP2 = AP2.
Passo 2
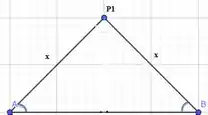
Para saber se P1P2 divide AB pela metade podemos analisar o triângulo AP1B. O triângulo é isósceles, por possuir dois lados iguais e, consequentemente, seus ângulos da base também são iguais:
Da mesma forma, se analisarmos o triângulo P1BP2 observamos que também é isósceles:
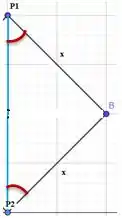
Então:
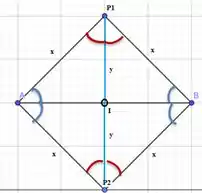
Se observarmos os triângulos AP1I e BP1I são semelhantes e se encaixam no caso de semelhança LAL (lado-ângulo-lado). Sendo assim, eles possuem três ângulos iguais e, portanto, três lados iguais. Podemos concluir então que:
Então o segmento P1P2 divide o segmento AB em duas partes iguais, ou seja, atravessa o ponto médio de AB.
Provado esta parte agora temos que provar que P1P2 é perpendicular a AB.
Passo 3
Para provar que o terceiro ângulo é igual a 90° devemos lembrar que os triângulos possuem os três ângulos iguais. Sendo assim:
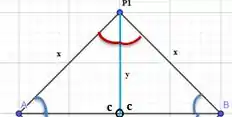
Então o segmento P1P2 corta o segmento AB com um ângulo de 90°, comprovando ser perpendicular.
Resposta
Ei, a resposta está no passo a passo :)