Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.3 - Ex. 38
A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método.
em torno do eixo
Passo 1
Usando discos temos o seguinte desenho:
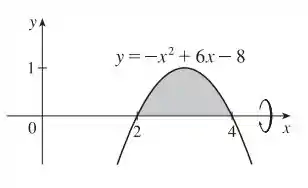
Passo 2
Temos o seguinte volume:
Resposta
.
Exercícios de Livros Relacionados
Nos exercícios 31-36, determine os volumes dos sólidos obtidos com a rotação das regiões em torno dos eixos dados. Se preferir, você poderá usar anéis para resolvê-los. 31 – O triângulo com vértices (
Nos exercícios 31-36, determine os volumes dos sólidos obtidos com a rotação das regiões em torno dos eixos dados. Se preferir, você poderá usar anéis para resolvê-los. 31 – O triângulo com vértices (
Para algumas regiões, os dois métodos funcionam bem para sólidos obtidos com a rotação da região em torno dos eixos das coordenadas, mas isso nem sempre ocorre. Por exemplo, quando uma região gira em
Para algumas regiões, os dois métodos funcionam bem para sólidos obtidos com a rotação da região em torno dos eixos das coordenadas, mas isso nem sempre ocorre. Por exemplo, quando uma região gira em
Para algumas regiões, os dois métodos funcionam bem para sólidos obtidos com a rotação da região em torno dos eixos das coordenadas, mas isso nem sempre ocorre. Por exemplo, quando uma região gira em