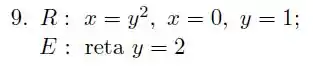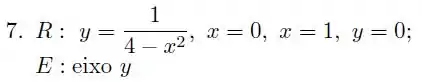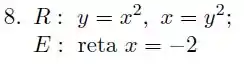Exercícios de Cascas Cilíndricas - Lista de Exercícios Resolvida
Questão 1
Encontre o volume obtido pela rotação da placa limitada por , , e , em torno do eixo , sendo .
Ver solução completaQuestão 2
Considere a região delimitada pelo gráfico da função e pelo eixo , com .
Calcule o volume do sólido de revolução obtido pela rotação dessa região em torno do eixo .
Ver solução completaQuestão 3
Seja a região compreendida entre os gráficos de e para , como mostra a figura abaixo:
Calcule o volume do sólido obtido pela rotação de em torno de .
Ver solução completaQuestão 4
Seja a região situada entre as curvas , , e . Calcule o volume do sólido obtido fazendo girar a região em torno do eixo .
Ver solução completaQuestão 5
Considere a região delimitada pela parábola e pela reta .
Considere o sólido obtido pela rotação da região ao redor da reta . Escreva uma integral que calcule o volume de .
Calcule o Volume de .
Ver solução completaQuestão 6
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação, em torno do eixo y, das regiões limitadas pelas curvas e retas a seguir:
Ver solução completaQuestão 7
Calcule o volume do sólido obtido pela rotação em torno do eixo da região delimitada pela curva , e .
Ver solução completaQuestão 8
Seja . Determine o volume do sólido obtido pela rotação de em torno do eixo .
Ver solução completaQuestão 9
Encontre as dimensões do cilindro circular reto de maior volume que pode ser inscrito num cone circular reto com raio de 3 m e de altura 5 m.
Ver solução completaQuestão 10
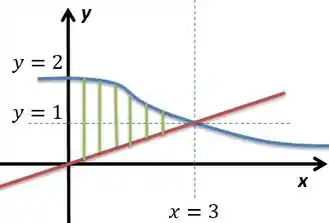
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação da região sombreada em torno do eixo :
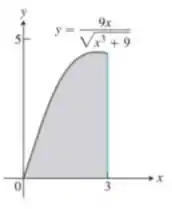
Questão 11
Encontre o volume obtido pela rotação da placa limitada por , , e , em torno do eixo , sendo .
Ver solução completaQuestão 12
Considere a região delimitada pela parábola e pela reta .
Esboce a região
Considere o sólido obtido pela rotação da região ao redor da reta . Escreva uma integral que calcule o volume de .
Calcule o Volume de .
Ver solução completaQuestão 13
Seja . Considere a região ilimitada , entre o eixo , o gráfico de , a reta e a reta . Calcule, se possível, o volume obtido pela rotação de ao redor da reta .
Ver solução completaQuestão 14
Use o método das cascas cilíndricas para encontrar o volume da região gerada pela rotação em torno do eixo x da região delimitada pelas curvas abaixo:
Questão 15
Seja a região compreendida entre os gráficos de e para , como mostra a figura abaixo:
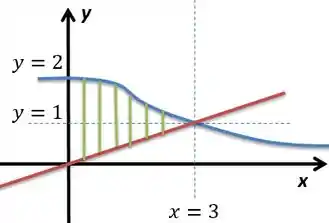
Calcule o volume do sólido obtido pela rotação de em torno de .
Calcule o volume do sólido obtido pela rotação de em torno de .
Ver solução completaQuestão 17
Seja a região delimitada pelas curvas ,
Esboce a região
Determine a área da região
Calcule o volume do sólido obtido pela rotação desta região ao redor da reta
Ver solução completaQuestão 18
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação da região sombreada em torno do eixo :
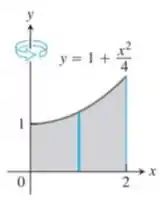
Questão 19
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e largura. Então, escreva a integral que dá o volume do sólido de rotação dessa área em torno das retas dadas. Em, pelo menos um dos volumes deve ser usado o método das cascas cilíndricas.
Ver solução completaQuestão 20
Fixado considere a região delimitada pelas curvas e . Considere também o sólido dado pela rotação de em torno do eixo . Se é a área de e é o volume de , então:
- não depende de e é diretamente proporcional a
- é diretamente proporcional a e é diretamente proporcional a
- é diretamente proporcional a e é diretamente proporcional a
- e são diretamente proporcionais a
- e são diretamente proporcionais a
Questão 21
A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método.
a. em torno do eixo x
Ver solução completaQuestão 22
Nos seguintes itens determine os volumes dos sólidos obtidos com a rotação das regiões em torno dos eixos dados.
b) A região delimitada por , , em torno
(i) da reta
(ii) da reta .
Ver solução completaQuestão 23
Considere a região plana definida por
Seja o sólido de revolução obtido pela rotação de em torno do eixo .
Letra b) Calcule o volume de pelo método que preferir.
Ver solução completaQuestão 24
Considere a região plana definida por:
(a.1) Esboce a região plana
(a.2) Escreva a área da região como uma integral na variável
(a.3) Escreva a área da região como uma soma de integrais na variável
Seja um sóldio de revolução obtido pela rotação da região em torno do eixo
(b.1) Utilizando o Método de Discos, escreva o volume de como uma integral na variável
(b.2) Utilizando o Método de Cascas Cilíndricas, escreva o volume de como uma soma de integrais na variável
(b.3) Calcule o volume de pelo método que preferir
Ver solução completaQuestão 25
5) Calcule o volume do sólido obtido pela rotação ao redor do eixo da área finita delimitada pelas curvas e
Ver solução completaQuestão 26
Considere a região plana definida por:
Seja o sólido de revolução obtido pela rotação de em torno do eixo
- Esboce abaixo a região plana
- Utilizando o Método dos Discos, determine uma soma de duas integrais que forneça o volume de . Obs: Nesse item não é necessário calcular a integral
- Utilizando o Método de Cascas, determine uma integral que forneça o volume de . Obs: Nesse item não é necessário calcular a integral
- Calcule o volume de pelo método que preferir
Questão 27
Considere as funções e e a região plana descrita abaixo:
Seja o sólido de revolução obtido pela rotação de em torno do eixo
- Esboce a região
- Determine e (as expressões das funções inversas de e , respectivamente)
- Utilizando o método que preferir, escreva o volume de como uma integral ou soma de integrais. Obs.: Neste item não é necessário calcular o volume
Questão 28
Use o método das cascas cilíndricas para encontrar o volume da região gerada pela rotação em torno do eixo y da região delimitada pelas curvas abaixo:
Questão 29
4. Encontre o valor da área delimitada pelo gráfico da função , o eixo e as retas verticais e .
Ver solução completaQuestão 30
3. Calcule o VOLUME do sólido obtido pela rotação ao redor do EIXO Y da região delimitada pelos gráficos de , e as retas verticais e .
Ver solução completaQuestão 31
Seja uma função contínua e a região compreendida entre o gráfico de e o eixo . Quando giramos a região em torno do eixo , obtemos um sólido de revolução cujo volume é dado por . Calcule esse volume no caso as funções indicadas abaixo
Ver solução completaQuestão 32
Use o método das cascas cilíndricas para calcular o volume do sólido obtido rotacionando a região em torno do eixo . Esboce o sólido obtido.
a) é limitada por baixo pelo eixo e acima por entre .
Ver solução completaQuestão 33
Use o método das cascas cilíndricas para calcular o volume do sólido obtido rotacionando a região em torno do eixo . Esboce o sólido obtido.
b) é limitada por baixo pelo eixo , a direita pela reta e acima por entre .
Ver solução completaQuestão 34
12. Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação, em torno do eixo das regiões limitadas pelas curvas e retas a seguir:
e)
Ver solução completaQuestão 35
12. Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir:
f)
Ver solução completaQuestão 36
Encontre o volume do sólido que permanece depois que um furo circular de um raio é perfurado através do centro de uma esfera sólida de raio por:
b) Cascas cilindricas
Ver solução completaQuestão 37
12. Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir:
g)
Ver solução completaQuestão 38
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação, em torno do eixo y, das regiões limitadas pelas curvas e retas a seguir:
Ver solução completaQuestão 39
Deduza a fórmula do volume do toro obtido ao giramos o circulo em torno do eixo x
Ver solução completaQuestão 40
Use o método da casca para determinar o volume dos sólidos obtidos com a rotação da região sombreada em torno do eixo indicado:
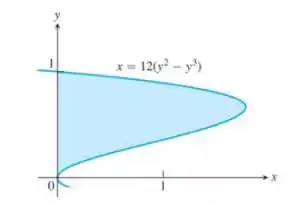
reta
Ver solução completaQuestão 41
Use o método da casca para determinar o volume dos sólidos obtidos com a rotação da região sombreada em torno do eixo indicado:
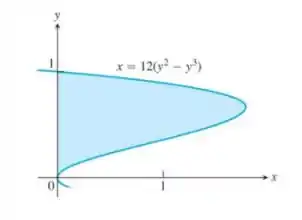
reta
Ver solução completaQuestão 42
Use o método das cascas cilíndricas para encontrar o volume da região gerada pela rotação em torno do eixo x da região delimitada pelas curvas abaixo:
b)
Ver solução completaQuestão 43
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação da região sombreada em torno do eixo x:
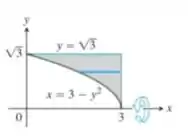
Questão 44
12. Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir:
h)
Ver solução completaQuestão 45
12. Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação, em torno do eixo, das regiões limitadas pelas curvas e retas a seguir:
d)
Ver solução completaQuestão 46
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e largura. Então, escreva a integral que dá o volume do sólido de rotação dessa área em torno das retas dadas. Em, pelo menos um dos volumes deve ser usado o método das cascas cilíndricas.
Ver solução completaQuestão 47
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir:
Ver solução completaQuestão 48
Calcule o volume do sólido obtido com a rotação da região triangular limitada pelas retas , e , em torno:
do eixo , usando o método da casca.
Ver solução completaQuestão 49
A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método.
b. em torno do eixo y.
Ver solução completaQuestão 50
A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método.
c.em torno do eixo y.
Ver solução completaQuestão 51
Considere a região delimitada pelas curvas , ,
- Esboce a região .
- Escreva a integral, ou soma de integrais, que determina(m) o volume sólido obtido pela rotação da região acima ao redor do eixo .
- Calcule o volume do sólido do item acima.
Questão 52
A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método.
d., , ; em torno do eixo y.
Ver solução completaQuestão 53
Nos seguintes itens determine os volumes dos sólidos obtidos com a rotação das regiões em torno dos eixos dados.
a) O triangulo com vértices , e
em torno:
i)Da reta .
Ver solução completaQuestão 54
Seja a região delimitada pelas curvas e
- Esboce a região
- Escreva a integral, ou soma de integrais, que determina(m) o volume do sólido obtido pela rotação da região acima ao redor da reta
- Calcule o volume da sólido do item acima.
Questão 55
Determine o volume do sólido obtido pela rotação, em torno da reta , da região
Ver solução completaQuestão 56
Seja o sólido obtido pela rotação da região delimitada pelas curvas e em torno da reta . Qual é o volume desse sólido?
a)
b)
c)
d)
e)
Ver solução completaQuestão 57
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e largura. Então, escreva a integral que dá o volume do sólido de rotação dessa área em torno das retas dadas. Em, pelo menos um dos volumes deve ser usado o método das cascas cilíndricas.
Ver solução completaQuestão 58
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e largura. Então, escreva a integral que dá o volume do sólido de rotação dessa área em torno das retas dadas. Em, pelo menos um dos volumes deve ser usado o método das cascas cilíndricas.
Ver solução completaQuestão 59
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e largura. Então, escreva a integral que dá o volume do sólido de rotação dessa área em torno das retas dadas. Em, pelo menos um dos volumes deve ser usado o método das cascas cilíndricas.
Ver solução completaQuestão 60
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e largura. Então, escreva a integral que dá o volume do sólido de rotação dessa área em torno das retas dadas. Em, pelo menos um dos volumes deve ser usado o método das cascas cilíndricas.
Ver solução completaQuestão 61
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e largura. Então, escreva a integral que dá o volume do sólido de rotação dessa área em torno das retas dadas. Em, pelo menos um dos volumes deve ser usado o método das cascas cilíndricas.
Ver solução completaQuestão 62
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e largura. Então, escreva a integral que dá o volume do sólido de rotação dessa área em torno das retas dadas. Em, pelo menos um dos volumes deve ser usado o método das cascas cilíndricas.
Ver solução completaQuestão 63
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e largura. Então, escreva a integral que dá o volume do sólido de rotação dessa área em torno das retas dadas. Em, pelo menos um dos volumes deve ser usado o método das cascas cilíndricas.
Ver solução completaQuestão 64
Considere a região limitada pelas curvas , pelo eixo e pela reta .
Faça um esboço da região .
Escreva uma única integral que expresse a área da região . Não precisa calcular a integral.
Calcule o volume do sólido obtido pela rotação da região em torno do eixo .
Ver solução completaQuestão 65
Seja a região plana definida por:
Considere o sólido de revolução obtido através da rotação da região em torno do eixo .
(a) Esboce a região
(b) Usando o método que preferir, escreva o volume de S como uma integral ou como uma soma de integrais.
(c) Calcule o volume de S.
Ver solução completaQuestão 66
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e largura. Então, escreva a integral que dá o volume do sólido de rotação dessa área em torno das retas dadas. Em, pelo menos um dos volumes deve ser usado o método das cascas cilíndricas.
Ver solução completaQuestão 67
Use o método da casca para determinar o volume dos sólidos obtidos com a rotação da região sombreada em torno do eixo indicado:
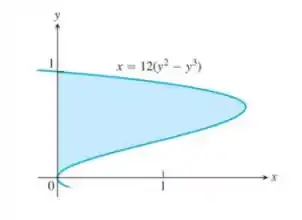
reta
Ver solução completaQuestão 68
Encontre o volume gerado pela rotação da região limitada
em torno da reta .
Ver solução completaQuestão 69
13. Use o método da casca para determinar o volume dos sólidos obtidos com a rotação da região sombreada em torno do eixo indicado:
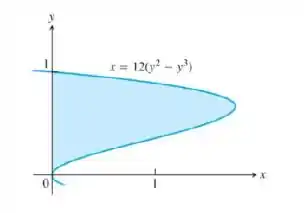
a) eixo
Ver solução completaQuestão 70
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação da região sombreada em torno do eixo :
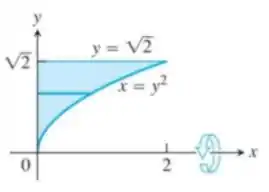
Questão 71
Utilize o método da casca cilíndrica para determinar o volume do sólido gerado pela rotação da região limitada por:
, em torno do eixo y.
Ver solução completaQuestão 72
Utilize o método da casca cilíndrica para determinar o volume do sólido gerado pela rotação da região limitada por:
, em torno do eixo y.
Ver solução completaQuestão 73
Utilize o método da casca cilíndrica para determinar o volume do sólido gerado pela rotação da região limitada por:
, em torno do eixo y.
Ver solução completaQuestão 74
Utilize o método da casca cilíndrica para determinar o volume do sólido gerado pela rotação da região limitada por:
, em torno do eixo y.
Ver solução completaQuestão 75
Utilize o método da casca cilíndrica para determinar o volume do sólido gerado pela rotação da região limitada por:
, em torno do eixo y.
Ver solução completaQuestão 76
Utilize o método da casca cilíndrica para determinar o volume do sólido gerado pela rotação da região limitada por:
, em torno do eixo y.
Ver solução completaQuestão 77
Utilize o método da casca cilíndrica para determinar o volume do sólido gerado pela rotação da região limitada por:
, ao redor da reta x=1.
Ver solução completaQuestão 78
Utilize o método da casca cilíndrica para determinar o volume do sólido gerado pela rotação da região limitada por:
, em torno do eixo x.
Ver solução completaQuestão 79
Utilize o método da casca cilíndrica para determinar o volume do sólido gerado pela rotação da região limitada por:
, em torno do eixo x.
Ver solução completaQuestão 80
Use o método das cascas cilíndricas para encontrar o volume da região gerada pela rotação em torno do eixo y da região delimitada pelas curvas abaixo:
b)
Ver solução completaQuestão 81
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação da região sombreada em torno do eixo :
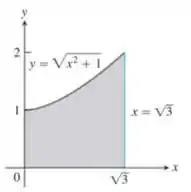
Questão 82
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação, em torno do eixo y, das regiões limitadas pelas curvas e retas a seguir:
Ver solução completaQuestão 84
Ache o volume gerado pela rotação em torno do eixo da placa definida por:
Ver solução completaQuestão 85
Use o método das cascas cilíndricas para encontrar o volume da região gerada pela rotação em torno do eixo y da região delimitada pelas curvas abaixo:
c)
Ver solução completaQuestão 86
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir:
Ver solução completaQuestão 88
Utilize o método da casca cilíndrica para determinar o volume do sólido gerado pela rotação da região limitada por:
, em torno do eixo y.
Ver solução completaQuestão 89
Utilize o método da casca cilíndrica para determinar o volume do sólido gerado pela rotação da região limitada por:
, em torno do eixo y.
Ver solução completaQuestão 90
Utilize o método da casca cilíndrica para determinar o volume do sólido gerado pela rotação da região limitada por:
, ao redor da reta y=3.
Ver solução completaQuestão 91
Utilize o método da casca cilíndrica para determinar o volume do sólido gerado pela rotação da região limitada por:
, em torno da reta y=2.
Ver solução completaQuestão 92
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação, em torno do eixo y, das regiões limitadas pelas curvas e retas a seguir:
Ver solução completaQuestão 93
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir:
Ver solução completaQuestão 94
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação, em torno do eixo y, das regiões limitadas pelas curvas e retas a seguir:
Ver solução completaQuestão 96
3. Calcule as seguintes integrais de linha ao longo do caminho indicado:
(c) ao longo da rela .
Ver solução completaQuestão 97
3. Calcule as seguintes integrais de linha ao longo do caminho indicado:
(d) ; .
Ver solução completaQuestão 98
(4) Utilize o Teorema de Pappus-Guldin para determinar:
(a) o volume do sólido de revolução gerado pela rotação do hexágono regular inscrito no círculo ao redor do eixo .
Ver solução completaQuestão 99
(4) Utilize o Teorema de Pappus-Guldin para determinar:
(c) o centroide da região .
Ver solução completaQuestão 100
Utilize o método da casca cilíndrica para determinar o volume do sólido gerado pela rotação da região limitada por:
, em torno do eixo y.
Ver solução completaQuestão 101
Seja a região situada entre as curvas , , e . Calcule o volume do sólido obtido fazendo girar a região em torno do eixo .
Ver solução completaQuestão 102
Em cada um dos exercícios a considere a região limitada pelas curvas de equações dadas. Calcule, por dois métodos distintos, o volume do sólido obtido pela rotação da em torno do eixo dado.
Ver solução completa
Questão 103
Seja definida em e a região delimitada pelo gráfico da função e o eixo . Calcule o volume do sólido gerado ao se rotacionar a região ao redor do eixo .
Ver solução completaQuestão 104
Em cada um dos exercícios a considere a região limitada pelas curvas de equações dadas. Aplicando o método das cascas cilíndricas, calcule o volume do sólido obtido pela rotação da região em torno do eixo dado.
Ver solução completa
Questão 105
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e largura. Então, escreva a integral que dá o volume do sólido de rotação dessa área em torno das retas dadas. Em, pelo menos um dos volumes deve ser usado o método das cascas cilíndricas.
Ver solução completaQuestão 106
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e largura. Então, escreva a integral que dá o volume do sólido de rotação dessa área em torno das retas dadas. Em, pelo menos um dos volumes deve ser usado o método das cascas cilíndricas.
Ver solução completaQuestão 107
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e largura. Então, escreva a integral que dá o volume do sólido de rotação dessa área em torno das retas dadas. Em, pelo menos um dos volumes deve ser usado o método das cascas cilíndricas.
Ver solução completaQuestão 108
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação da região sombreada em torno do eixo :
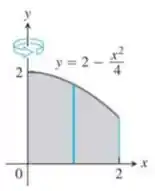
Questão 109
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e largura. Então, escreva a integral que dá o volume do sólido de rotação dessa área em torno das retas dadas. Em, pelo menos um dos volumes deve ser usado o método das cascas cilíndricas.
Ver solução completaQuestão 110
Q03) Considere a região plana definida por:
Seja o sólido de revolução obtido pela rotação de em torno do eixo
- Esboce abaixo a região plana
- Utilizando o Método de Discos, determine uma integral que forneça o volume de
- Utilizando o Método de Cascas, determine uma integral que forneça o volume de
- Calcule o volume de pelo método que preferir.