Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.2 - Ex. 29b
Para algumas regiões, os dois métodos funcionam bem para sólidos obtidos com a rotação da região em torno dos eixos das coordenadas, mas isso nem sempre ocorre. Por exemplo, quando uma região gira em torno do eixo y e anéis são usados, devemos integrar em relação a y. No entanto, pode não ser possível expressar o integrando em termos de y . Em tais casos, o método da casca permite integrar em relação a x em vez de y. Os Exercícios 29 e 30 fornecem uma compreensão clara disso.
29 – Calcule o volume do sólido obtido com a rotação em tomo de cada eixo coordenado da região limitada por y = e y = , usando:
B – O método do anel.
Passo 1
Antes de realizar o que se pede, iremos plotar o gráfico das funções dadas, assim teremos esta figura que segue os limites de 1 e 0.
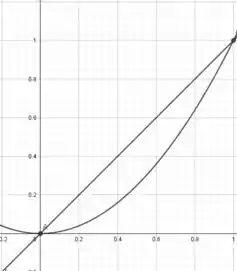
Desta forma utilizaremos primeiro o método do anel em torno do eixo x e depois em torno do eixo y.
Passo 2
Primeiramente vamos verificar as funções para o eixo x.
Assim é verificado para este método.
Utilizando a fórmula:
Inserindo na fórmula teremos:
Resolvendo a integral teremos:
Inserindo os limites de integração, obteremos o volume:
Resolvendo:
Tirando o mínimo múltiplo comum e resolver as frações:
Observação: Como pediu o volume e não foi informado uma unidade de medida utilizamos o termo que significa unidade de volume.
Passo 3
Em torno do eixo y.
Precisaremos encontrar a função em relação a y.
Inserindo na fórmula:
Resolvendo as integrais:
Substituindo os limites de integração:
Assim:
Resposta
Em torno do eixo x =
Em torno do eixo y =