Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 56

Represente graficamente as equações dos Exercícios 9-58 seguindo os passos do procedimento para construção de gráficos da página 237. Inclua as coordenadas de quaisquer pontos extremos e absolutos locais e pontos de inflexão.

56-

y = ln ⁡ x x

Passo 1

Fazendo a primeira derivada temos:

y ' = ( ln ⁡ x ) ' ( x ) - ( ln ⁡ x ) ( x ) ' x

y ' = x x - ln ⁡ x 2 x x

y ' = x x 2 - ln ⁡ x 2 x 3 2

y ' = 2 x - x l n   x 2 x 2 x

y ' = 2 - ln ⁡ x 2 x 3 2 = 1 x 3 2 - ln ⁡ x 2 x 3 2

Agora fazendo a segunda derivada :

y ' ' = - 3 2   x - 5 2 - 1 2 ( ln ⁡ x ) ' ( x 3 2 ) - ( x 3 2 ) ' ( ln ⁡ x )   x 3

y ' ' = - 8 + 3 ln ⁡ x 4 x 5 2

Note que tanto o l n ⁡ ( x ) quanto x não aceitam termos negativos ou zero.

Passo 2

Pontos críticos:

Fazendo y ' = 0

2 - ln ⁡ x = 0 → x = e 2

Passo 3

Testando os valores de máximo e mínimo e verificando pontos de inflexão:

y ' ' e 2 = - 8 + 3   l n ⁡ ( e 2 ) 4 × e 2 × 5 2 = - 8 + 6 4 e 5 = - 1 2 e 5 → n e g a t i v o

Logo x= e 2 é o ponto de máximo

Ponto de inflexão:

Fazendo y ' ' = 0

- 8 + 3 ln ⁡ x = 0

x = e 8 3

Passo 4

Verificar os limites:

Para zero a direita:

lim x → 0 + ⁡ ln ⁡ x x = ln ⁡ x × 1 x  

O que dá:

- ∞ × ∞ = - ∞

Para mais infinito:

lim x → ∞ ⁡ ln ⁡ x x = ∞ ∞

Fazendo L’Hopital:

lim x → ∞ ⁡ 1 x 1 2 x → lim x → ∞ ⁡ 2 x x = ∞ ∞

Fazendo L’Hopital de novo:

lim x → ∞ ⁡ 1 x = 0

Passo 5

Agora organizando nossos intervalos temos:

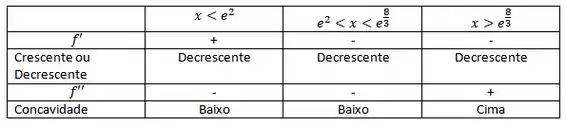
Valores de teste: 1,10,15

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais e verticais e dê suas equações. Identifique (se houver)
Obtenha um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais e verticais e dê suas equações. Identifique (se houver)
Obtenha um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais e verticais e dê suas equações. Identifique (se houver)
Obtenha um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais e verticais e dê suas equações. Identifique (se houver)
Obtenha um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais e verticais e dê suas equações. Identifique (se houver)