Represente graficamente as equações dos Exercícios 9-58 seguindo os passos do procedimento para construção de gráficos da página 237. Inclua as coordenadas de quaisquer pontos extremos e absolutos locais e pontos de inflexão.

42-

Como não temos nenhum denominador na função e sua derivada primeira não tem uma função par no denominador não temos assíntotas verticais. Então temos que nos preocupar em achar somente os pontos críticos .

Porém essa função é peculiar. Olha só

Vamos fazer o que sempre fizemos

Prosseguimos com a ideia de que esse ponto é um ponto de máximo ou mínimo.

Porém devo me atentar ao seu denominador pois se x for igual a -1 eu terei um crescimento infinito. Então eu devo sim tratar esse ponto de forma diferenciada pois não tem como afirmar o que esse ponto de fato é.

Agora para a derivada segunda:

Opa! Esse ponto pode representar uma singularidade ou uma inflexão, tudo depende do sinal da derivada segunda antes ou após esse valor.

Para , o mesmo fenômeno ocorre, então realmente devemos trata-lo como um ponto a ser analisado.

Como não temos assíntotas verticais vamos apenas ver se existe as horizontais.

Então a função surge de – infinito e vai até infinito

Organizando nossos intervalos:

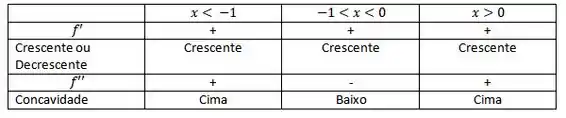
Valores de teste para x: -2,-0.5,1

Então temos e como pontos de inflexão da função por conta da troca de concavidade da função , não tendo nenhum ponto de máximo e mínimo absoluto.

Isso se deve em conta do grau da função que é de 1, é como se tivesse sendo feito

O que acaba em valores maiores que 1 se comportando como uma função linear.