Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 46
Represente graficamente as equações dos Exercícios 9-58 seguindo os passos do procedimento para construção de gráficos da página 237. Inclua as coordenadas de quaisquer pontos extremos e absolutos locais e pontos de inflexão.
46-
Passo 1
Pela 45 a gente consegue ter noção do gráfico pois é parecida com aquela só que deslocada para a direita. Vamos começar dividindo nosso módulo.
Porém por estar deslocada a direita e não estar tão simétrico em relação ao eixo y como a função estava na questão 45 fica de difícil compreensão escrever na mesma notação que foi usada na questão 45. Então precisamos saber dos intervalos em que há mudança de sinal. Para isso precisamos saber suas raízes que são:
E depois saber como esse gráfico se comporta. Pois dai saberemos que entre 0 e 2 a função é negativa. Logo teremos:
Derivando agora todas essas funções temos:
Fazendo a derivada segunda:
Passo 2
Analisando a primeira derivada da função nós temos:
Que em x=1 temos um ponto crítico da função , além é claro dos intervalos que delimitamos no passo anterior.
Passo 3
Como x está dentro do intervalo conseguimos dizer que pela derivada segunda no mesmo intervalo ser de -2 que esse ponto é um máximo local.
Passo 4
O próximo passo seria aplicar o limite para porém é fácil ver que em uma função par como essa para as duas situações a função tenderá a
Logo basta organizar nossos intervalos:
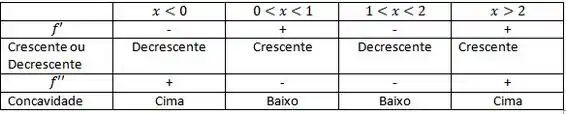
Resposta
Ei, a resposta está no passo a passo :)