Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.4 - Ex. 7
Seja com e tome . Use um recurso gráfico e sua operação de traçar retas para encontrar um número positivo , tal que se .
Passo 1
Então pessoal, se plotarmos o gráfico de teremos:
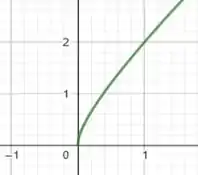
E desse mesmo gráfico conseguimos tirar os pontos:
Como temos dois valores de e dois valores de , podemos definir e .
Passo 2
Como o gráfico cresce, então podemos dizer que , logo:
Arredondando para facilitar nossa vida:
Sendo assim, podemos tomar um delta mínimo, tal que:
E essa é a nossa resposta, galera!
Resposta
Exercícios de Livros Relacionados
Prove que lim x → 4 - 2 x - 4 2 = - ∞ Usando a definição 2.4 . 2 Definição 2.4 . 2 :Seja f uma função definida em todo número de um intervalo aberto I contendo a , exceto possivelmente no próprio a
Prove que lim x → 2 3 x - 2 2 = + ∞ Usando a definição 2.4 . 1 Definição 2.4 . 1 :Seja f uma função definida em todo número de um intervalo aberto I contendo a , exceto possivelmente no próprio a .
Para cada uma das funções a seguir, ache a assíntota vertical do gráfico e faça um esboço dele: f x = 4 x - 5 2
Use a definição 2.4 . 1 para provar que lim x → - 3 5 - x 3 + x = + ∞ Definição 2.4 . 1 :Seja f uma função definida em todo número de um intervalo aberto I contendo a , exceto possivelmente no própr
Para cada uma das funções a seguir, ache a assíntota vertical do gráfico e faça um esboço dele: f x = 5 x 2 + 8 x + 15