Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.5 - Ex. 14

Seja g x =   tan 2 ⁡ x x 1     0 , x ≤ π 4

  1. Mostre que x g x = ( tan ⁡ x ) 2   ; 0 ≤ x ≤ π 4
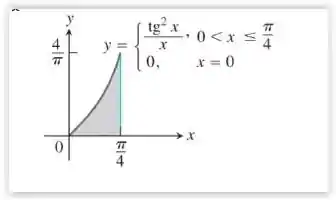
  2. Determine o volume do sólido obtido com a rotação da região sombreada em torno do eixo y na figura a seguir:

Passo 1

  1. Temos a seguinte imagem gráfica:

    2. como g x = tan 2 ⁡ x x logo,

    x g x = x .   tan 2 ⁡ x x .  

    Simplificamos x e ficamos como x g x = tan 2 ⁡ x variado no intervalo 0 < x ≤ π 4 , desde que tan  ⁡ 0 = 0 , temos 0   e m   x = 0 .

    Passo 2

  2. estamos diante do método da casca cilíndrica, ou seja podemos integrar de x = a a x = b e obteremos o volume fazendo:

V =   ∫ a b 2 π x   f x d x

Substituindo pelos dados fornecidos, temos:

V =   ∫ 0 π 4 2 π tan 2 ⁡ x d x = 2 π ∫ 0 π 4 tan 2 ⁡ x d x

Devemos lembrar da seguinte identidade trigonométrica, para realizar a substituição:

tan 2 ⁡ x = sec 2 ⁡ x - 1    

Logo,

= 2 π ∫ 0 π 4 ( sec 2 ⁡ x - 1   ) ⁡ d x = 2 π   [ tan ⁡ x - x   ]   | π 4 0

= 2 π 1 - π 4 =   4 π - π 2 2

Resposta

4 π - π 2 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o método da casca para determinar o volume dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir: x =y; x = - y ; y = 2
Use o método da casca para determinar o volume dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir: x =y 2 ; x = - y ; y = 2 ; y0
13. Bombeamento de água O tanque retangular mostrado aqui, com o seu topo ao nível do solo, é usado para captar água pluvial. Considere que o peso específico da água seja 62,4l b / p é 3 é .a. Quando
Use o método da casca para determinar o volume dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir: x =2 y - y 2 ; x = 0