Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.5 - Ex. 13
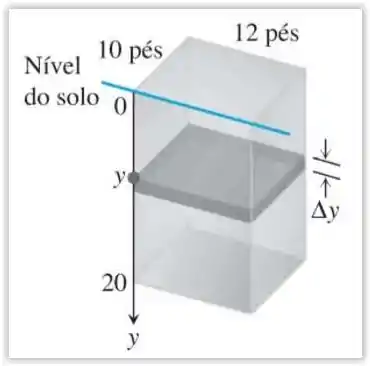
13. Bombeamento de água O tanque retangular mostrado aqui, com o seu topo ao nível do solo, é usado para captar água pluvial. Considere que o peso específico da água seja .
a. Quando o tanque estiver cheio, quanto trabalho será necessário para esvaziá-lo bombeando a água de volta ao nível do solo?
b. Se a água for bombeada para o nível do solo com motor de (potência ), quanto tempo levará para esvaziar o tanque cheio (arredonde para o minuto mais próximo)?
c. Mostre que a bomba no item (b) reduzirá o nível de água em 10 pés (metade) durante os primeiros 25 min de bombeamento.
d. Peso da água Quais são as respostas para os itens (a) e (b) em um local onde o peso específico da água seja ? E ?
Passo 1
O item a pede para gente calcular o quanto de trabalho é necessário para esvaziar o tanque cheio.
Passo 2
Lembrando que para calcular o trabalho usamos .
Vamos descobrir quem é nosso .
O exercício nos diz que a massa específica da água é , repare que isso é uma unidade de Força () dividida por uma unidade de volume, ou seja, se multiplicarmos isso pelo volume da água teremos unidade de força, então
Agora vamos descobrir quem é nosso .
O volume da água no tanque será a multiplicação de suas arestas, ou seja
Nós ainda não sabemos o valor de porque o volume de água varia com o tempo, então também vai variar.
Passo 3
Legal, agora temos a força ( , e a distância (), e já podemos calcular o trabalho.
Repare que o trabalho será uma somatória de vários trabalhos, pois a massa varia com a posição, então
Essa integral resulta em
Passo 4
Agora vamos começar a resolver o segundo item.
O item b pede para gente calcular o quanto tempo é necessário para bombear a água para o nível do solo com o motor de de potência.
Passo 5
Vamos começar lembrando que a potência e calculada da seguinte forma
Basta agora isolar o tempo
Isso nos dá
Passo 6
Esse tempo que descobrimos está em segundos, para passa-lo para horas basta dividir por 3600
Agora para ficar melhor ainda nossa resposta, vamos multiplicar 0,664 por 60 para descobrir quantos minutos 0,664 horas representa
Então vamos chegar no resultado de 1 hora e 40 minutos.
Passo 7
Agora vamos para o terceiro item.
O item (c) pede para mostrar que a bomba no caso do item (b) reduzirá o nível da água plea metade nos primeiros 25 min.
Passo 8
Para descobrir isso vamos primeiro calcular o trabalho realizado até o tanque esvaziar metade.
Passo 9
Agora podemos descobrir o tempo, pois sabemos o trabalho e a potência
Mas esse tempo está em segundos, então basta dividir por 60, e assim convertemos para minutos
Passo 10
Finalmente o último item.
O item (d) pede para calcular as respostas do item (a) e (b) mas no caso onde o peso específico sejam e
Passo 11
Vamos começar com o item (a)
Para Massa específica de
Agora é só resolver essa integral
E para massa específica de
Agora é só resolver essa integral
Passo 12
Agora o item (b)
Para Massa específica de temos que
Então podemos calcular o tempo dessa forma
Convertendo isso teremos aproximadamente 1 hora e 40 minutos também
Para Massa específica de temos que
Então podemos calcular o tempo dessa forma
Convertendo isso teremos aproximadamente 1 hora e 40 minutos também
Resposta
Item a)
Item b) 1 hora e 40 minutos
Item d) e
Os outros resultados serão 1 hora e 40 minutos aproximadamente