Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 70
Simplifique a expressão
Passo 1
Eaee, belezinha?? Bom... queremos simplificar a seguinte expressão:
Para isso, devemos lembrar das relações trigonométricas num triângulo retângulo. Veja só:
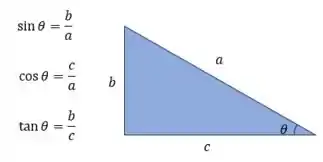
Agora vamos lá!! 😉
Passo 2
Se chamarmos
Temos que
Então, podemos montar um triangulo retângulo que nos dê a relação escrita acima
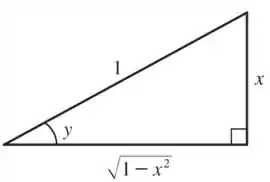
Passo 3
Agora, podemos tirar a tangente:
Entendeu direitinho?? Responde aee 😉
Resposta
Exercícios de Livros Relacionados
Cada um dos Exercícios 11-16 apresenta o gráfico de uma função y = f ( x ) . Copie o gráfico e sobreponha-o à reta y = x . Em seguida, utilize a simetria com relação à reta y = x para adicionar o gráf
Quais funções representadas graficamente nos Exercícios 1-6 são injetoras e quais não são?
Nos Exercícios 7-10, identifique, a partir de seu gráfico, se a função é injetora.8. f x = 2 x + 6 , x ≤ - 3 x + 4 , x- 3
Quais funções representadas graficamente nos Exercícios 1-6 são injetoras e quais não são?
Nos Exercícios 7-10, identifique, a partir de seu gráfico, se a função é injetora.9. f x = 1 - x 2 , x ≤ 0 x x + 2 , x0