Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 45
Suponha que a posição de uma partícula no instante seja dada por
E que a posição de uma segunda partícula seja dada por
a) Trace as trajetórias de ambas as partículas. Quantos pontos de interseção existem?
b) Alguns desses pontos de interseção são pontos de colisão? Em outras palavras, essas partículas algumas vez estão no mesmo lugar ao mesmo tempo? Se isso ocorrer, encontre os pontos de colisão.
c) Descreva o que acontecerá se a trajetória da segunda partícula for dada por
Passo 1
Fala ai pessoal, tranquilo! Vamos entender um pouco do que a questão está pedindo, e como podemos resolver?
O problema envolve a análise das trajetórias de duas partículas. E temos que verificar as trajetórias traçadas e a determinação dos pontos de interseção e colisão. Como faremos isso?
- 1° - Para saber se há alguma ponto de interseção teremos que identificar a curva de cada uma das equações, e assim que plotarmos o gráfico veremos a quantidade de pontos de interseção.
- 2° - Agora para saber se há pontos de colisão (colisão significa que as duas partículas ocupam a mesma posição no espaço ao mesmo tempo), teremos que igualar as trajetórias e vê se há algum instante que satisfaz o sistema.
- 3° - Depois é substituir na equação original e encontraremos o ponto em que há colisão.
Bingo! Vamos começar? 😊
Passo 2
a) Primeiro vamos identificar o que essas trajetórias representam né.
Vamos isolar o seno e cosseno nas parametrizações e identificar as curvas.
Para a primeira partícula temos:
Usando a relação fundamental da trigonometria:
E temos que a trajetória da primeira partícula representa uma elipse, com centro na origem e semieixo horizontal igual a 3 e semieixo vertical igual a 2.
Passo 3
Agora vamos fazer a mesma coisa para a trajetória da segunda partícula.
Relação fundamental da trigonometria:
E temos a equação de uma circunferência com centro em e raio 1.
Passo 4
Utilizando a equação encontrada no Passo (elipse) e do Passo (circunferência). Podemos identificar a quantidade de pontos de interseção.
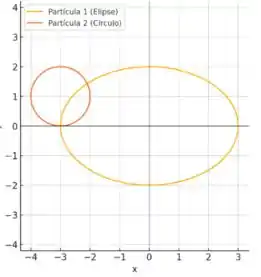
Vemos que há 2 pontos de interseção.
Passo 5
b) Agora vamos descobrir se há pontos de colisão.
Para isso é só igualar as trajetórias e vê se há algum instante que satisfaz o sistema.
Da primeira equação, tiramos que
Substituindo isso na segunda equação:
Logo, existe um ponto de colisão, que ocorre quando
E para descobrir esse ponto é só escolher uma das trajetórias e substituir:
Logo, as partículas colidem no o ponto .
Passo 6
c) Agora se a trajetória 2 fosse
Repara que só muda o sinal do em relação a trajetória anterior. Então ela continua sendo uma circunferência de raio , só que agora, o centro dela não está mais em , mas sim em .
O que significa que aquele desenho que fizemos no passo 3 estaria espelhado para a parte positiva do eixo . Mas as trajetórias continuariam se cruzando em dois pontos.
Show, até aí nada muda.
Passo 7
Agora vamos ver se muda algo em relação as partículas se colidirem. Vamos aplicar o mesmo procedimento que foi utilizado no Passo .
Igualando as trajetórias:
Da primeira equação, tiramos que
Substituindo isso na segunda equação:
E isso é impossível, posi não podemos definir o valor de , para encontrar o ponto de interseção. O que significa que se a trajetória fosse desse jeito que fala na letra , as partículas não iam se colidir.
Resposta
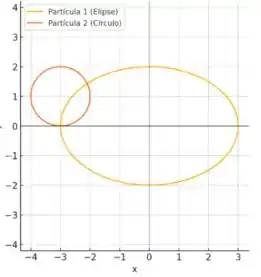
Há dois pontos de interseção.
As partículas colidem no o ponto .
As partículas não iam se colidir, mas continuariam tendo dois pontos de cruzamento.