Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.3 - Ex. 2
Suponha que seja uma função contínua, positiva e decrescente para e . Desenhando uma figura, coloque em ordem crescente as três quantidades
Passo 1
Fala, galera? Tranquilo?
Vamos entender primeiro o que são essas quantidades olhando nossa imagem:
é uma integral de uma função de 1 à 6, essa com a curva mostrada no desenho. Lembra do conceito de integral? Área abaixo da curva. Resumindo: essa integral representa a área abaixo da curva da função nesse intervalo.
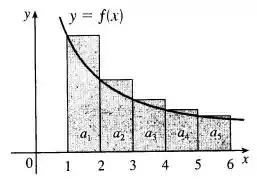
significa a soma dos retângulos de área , que juntos formam nossa série nesse intervalo (1° figura).
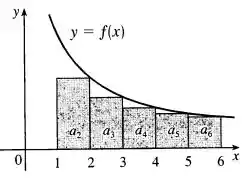
significa a soma dos triângulos de área que juntos formam nossa série nesse intervalo (2° figura).
Então, pessoal, nós vamos olhar essas imagens e comparar o valor de cada uma das suas séries com a área debaixo da curva de
Passo 2
Galera, vamos começar olhando nosso primeiro desenho:
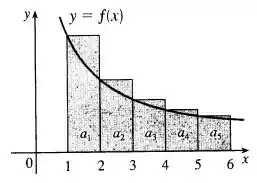
Perceba que ele mostra que os retângulos que representam a sequência de somas da série estão “para cima” da curva, estão sobrando. Ou seja, a área que teremos somando esses retângulos é maior que a área que temos abaixo da curva, então:
Passo 3
Agora vamos fazer outro desenho:
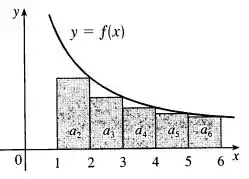
Olhando pra ele, vemos que temos justamente o contrário da figura anterior. Como os retângulos estão “para baixo” da curva, a soma desses retângulos que é a nossa série será menor que a área que realmente temos abaixo da curva, ou seja, nossa integral. Portanto:
Ou seja, podemos ordenar as quantidades assim: