Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.2 - Ex. 40
Três forças atuam sobre um objeto. Duas das forças estão a um ângulo de entre si e têm magnitudes de 25 N e 12 N. O terceiro é perpendicular ao plano das duas forças e tem magnitude 4 N. Calcule o valor da força que exatamente iria contrabalançar essas três forças
Passo 1
Temos que fazer um somatório de forças e igualar a 0. Para facilitar a nossa visualização, vamos fazer um esboço da distribuição dessas três forças.
Como não importa as posições delas, desde que seja mantido a relação de ângulos, vamos escolher posições que facilitem os nossos cálculos. Portanto, temos o seguinte esboço:
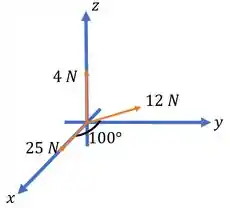
Percebam que tanto faz a escolha de quem é a força de 25 N ou a de 12 N. Isto apenas implica na direção final da nossa força, e não na sua magnitude.
Passo 2
Queremos determinar o valor de uma quarta força tal que, o somatório dela com as outras 3 deve ser nula. Portanto, vamos começar fazendo o somatório três das forças. Portanto,
A outra força é dada por:
Logo, a sua intensidade é: