Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.5 - Ex. 22
Faça o gráfico de ambas as sequências de termos e de somas parciais na mesma tela. Use o gráfico para fazer uma estimativa aproximada da soma da série. Em seguida, use o Teorema de Estimativa de Séries Alternadas para estimar a soma correta para quatro casas decimais.
Passo 1
E aí, pessoal? Firmeza?
Precisamos começar esboçando os gráficos. Vamos começar calculando alguns termos de e e depois vamos deixar que o software poupe nosso trabalho e trace os gráficos com mais pontos do que os que calculamos.
A partir do momento que obtivermos o gráfico, se o valor do somatório tender a uma reta horizontal, isto é, valor constante, verifica-se visualmente que a série é convergente.
Por fim, se queremos estimar a soma da série com quatro casa decimais, precisamos que o erro envolvido seja de 5 casas decimais. Para isto, precisamos determinar o valor de tal que:
Esse é o Teorema de Estimativa de Séries Alternadas.
Vamos lá!
Passo 2
Vamos começar calculando os termos da sequência e os termos da série manualmente:
A soma é dada por:
Bora! Para :
Para :
Para :
Para :
Para :
Ufa! Acho que deu pra entender o jeitão. Vamos deixar que o software mostre os demais resultados no nosso gráfico.
Passo 3
Vejamos inicialmente o gráfico contendo tanto a sequência de termos quanto as somas parciais.
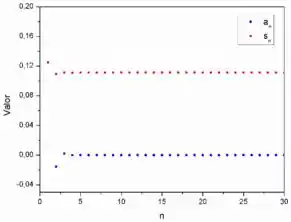
Como o valor de fica constante, podemos pegar o valor da coordenada de algum desses pontos, e assim obter que .
Passo 4
Para avaliarmos o Teste de Estimativa de Soma, vamos começar escrevendo os primeiros termos deste somatório. Portanto, a soma será
Nosso teorema diz que
Ou seja, que vamos precisar encontrar o último termo onde é maior que o erro 0,0001. Dos termos que escrevemos ali em cima, vamos encontrar o valor do sexto:
Como já está maior que o erro, o último termo que é menor que o erro é o termo anterior, ou seja, . Então, estimamos a soma parcial até .
Resposta
Pelo gráfico, estimamos que . Já a partir do teste de estimativa, temos