Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 7.3 - Ex. 37

Use o gráfico para aproximar as raízes da equação x 2 4 - x 2 = 2 - x . Então, aproxime a área limitada pela curva y = x 2 4 - x 2   e a reta y = 2 - x .

Passo 1

Vamos primeiro esboçar o gráfico

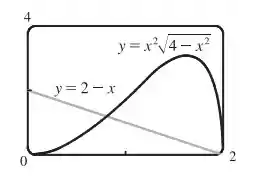
Pelo gráfico, podemos ver que as raízes da equação são x = a ≈ 0,81 e x = 2

Passo 2

Agora, vamos aproximar a área da seguinte forma. Pelo gráfico, vemos que x 2 4 - x 2 > 2 - x

Então, podemos aproximar a área

A ≈ ∫ a 2 x 2 4 - x 2 - 2 - x d x ≈ ∫ a 2 x 2 4 - x 2   d x - 2 x - 1 2 x 2 a 2

Vamos calcular a integral separadamente

∫ a 2 x 2 4 - x 2   d x

Seja x = 2 sin ⁡ θ , temos que d x = 2 cos ⁡ θ d θ . Vamos calcular os novos limites de integração

θ i n f e r i o r : a = 2 sin ⁡ θ ∴ θ = sin - 1 ⁡ a 2 = b

θ s u p e r i o r : 2 = 2 sin ⁡ θ ∴ θ = π / 2

∫ a 2 x 2 4 - x 2   d x = ∫ b π / 2 4 sin 2 ⁡ θ 4 - 4 sin 2 ⁡ θ 2 cos ⁡ θ d θ = ∫ b π 2 4 sin 2 ⁡ θ 4 cos 2 ⁡ θ 2 cos ⁡ θ d θ = ∫ b π 2 4 sin 2 ⁡ θ 2 cos ⁡ θ 2 cos ⁡ θ d θ = ∫ b π 2 4 sin 2 ⁡ θ 4 cos 2 ⁡ θ d θ = 4 ∫ b π 2 sin 2 ⁡ 2 θ d θ = 4 ∫ b π 2 1 2 1 - cos ⁡ 4 θ d θ = 2 θ - 1 4 sin ⁡ 4 θ b π 2 = 2 π 2 - 0 - b - 1 4 0,996 ≈ 2,81  

Passo 3

Agora, podemos calcular a área

A ≈ 2,81 - 2 ⋅ 2 - 1 2 ⋅ 2 2 - 2 a - 1 2 a 2 ≈ 2,10

Resposta

As raízes da equação são x = a ≈ 0,81 e x = 2

A ≈ 2,10

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da