Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.5 - Ex. 12
Use o método da casca cilíndrica para determinar o volume do sólido obtido com a rotação em torno do eixo y das regiões limitadas pelas curvas e retas a seguir:
Passo 1
Usamos o método da casca cilíndrica para calcular volumes de sólidos de revolução, ou seja, sólidos obtidos pela rotação de uma figura em torno de um eixo.
Podemos integras de a e obteremos o volume fazendo:
O enunciado nos fornece . Nos intervalos, . O que pode ser ilustrado pela imagem abaixo:
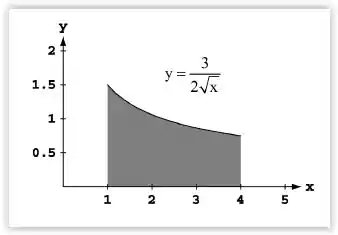
Vamos substituir na fórmula:
Resposta
Exercícios de Livros Relacionados
Uma balança para banheiro sofre uma compressão de 1 / 16 pol. quando uma pessoa de 150l b fica em pé sobre ela. Considerando que a balança se comporta como uma mola que obedece à Lei de Hooke, quando
Quanto trabalho foi necessário realizar sobre uma bola de softball com massa de 6,5 onças para lança-la de 132 pés/segundo ( 90milhas/hora)
Uma bola de Tênis com massa de 2 onças foi sacada a 160 pés/s (cerca de 109 mi/h). Qual o trabalho realizado sobre a bola para que ela atingisse essa velocidade?
Energia cinética Se uma força variável de magnitude F ( x ) desloca um corpo de massa m ao longo do eixo x de x 1 até x 2 ,a velocidade do corpo v pode ser escrita como d x d t dx/dt ( onde t represen