Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.3 - Ex. 35
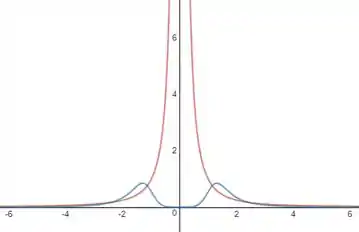
Utilize uma calculadora gráfica ou um computador para traçar na mesma tela a curva e sua função curvatura . Esse é o gráfico que você esperava?
Passo 1
Fala ai galerinha. Tranquilo? Vamos entender o que a questão pede e como faremos para resolver? Se liga ai! 😊
Vamos traçar a curvatura a curva na equação . Para isso
- Vamos utilizar a fórmula da curvatura
- Encontrar a primeira e a segunda derivada da equação .
- Substituir na fórmula, simplificar e colocar em uma calculadora gráfica a função e .
Agora é só resolver!
Passo 2
Para traçar o gráfico, primeiramente vamos calcular a curvatura usando a fórmula
Primeiramente calculando as derivadas
Substituindo na fórmula
Como um numero elevado a uma potência par é sempre positivo, podemos tirar do módulo.
Passo 3
Agora basta que joguemos em uma calculadora gráfica as equações de e
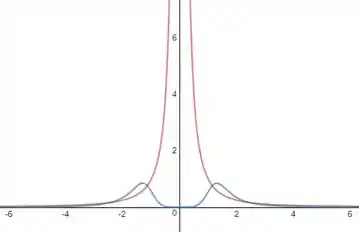
Em vermelho temos a curva de e em azul , onde temos pontos de máximo ou mínimo em .
Chegamos no resultado! Até a próxima! 😉
Resposta
