Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.2 - Ex. 2
(a) Faça um esboço grande da curva descrita pela função vetorial , e desenhe os vetores e .
(b) Desenhe o vetor começando em (1, 1) e comapare com o vetor
Explique porque esses vetores estão tão próximos um do outro tanto em módulo quanto em direção e sentido.
Passo 1
Inicialmente, queremos obter uma forma mais “familiar” para a função vetorial .
A curva descrita pela função vetorial dada pode ser representada pelas equações paramétricas
Isolando o parâmetro t nas duas equações temos
Do resultado obtido acima, sabemos que a curva representa uma função quadrática cuja forma é um “pedaço” de uma parábola com concavidade para a direita já que está limitado ao intervalo [0,2].
Passo 2
Os vetores podem ser obtidos substituindo-se os valores de da seguinte maneira:
OBS: utilizamos ponto e vírgula para separar os componentes do vetor pois já existem vírgulas separando algarismos de casas decimais. Dessa forma evitam-se confusões.
O vetor diferença pedido no enunciado é dado por
Passo 3
A imagem abaixo apresenta um esboço da curva juntamente com a representação dos vetores de posição e , e com o vetor .
Passo 4
Para obter o vetor basta derivar os componentes do vetor :
Assim, para , temos .
Por outro lado, temos
Passo 5
Uma representação dos dois vetores obtidos no passo anterior está mostrada abaixo, onde estes podem ser comparados.
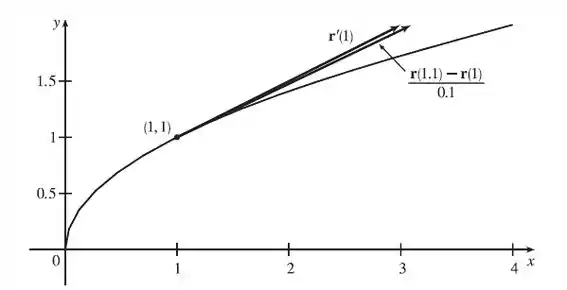
Passo 6
De fato, pela figura acima, observa-se que os vetores são muito próximos em módulo, direção e sentido.
Por definição a derivada de uma função vetorial é dada por
Para temos
Percebe-se com facilidade que o vetor calculado no final do passo 4 é igual à expressão dentro do limite anterior tomando-se .
Uma vez que 0,1 é próximo de 0, é previsível que tais vetores sejam semelhantes.
Resposta
Ei, a resposta está no passo a passo :)