Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.1 - Ex. 73
a) Para quais valores de a função
é derivável? Ache uma formula para
b) Esboce os gráficos de e .
Passo 1
Fala aí, galerinha!
Nesse problema queremos saber os valores de a função
é derivável e queremos tambem obter uma formula para .
E para fazer isso, o ideal é endender direitinho como essa função é definida de acordo com o seu domínio.
Podemos começar reescrevendo nossa função de modo a eliminar o modulo de .
Note que
para
Assim, podemos reescrevêla por partes, da seguinte forma:
Boa, para que a função seja derivável, sua derivada deve existir para cada um de seus ponto.
E vemos que os pontos que podem ter algum problema são, justamente, os extremos de cada intervalo.
Sendo assim, vamos analisar o comportamento da derivada nessas regiões.
Vem comigo que te mostro como fazer isso.
Veja só!
Passo 2
Vamos começar derivadno cada uma das funções que temos, e como todas elas são formada por polinômios e constantes, usaremos a informação de que a derivada de uma constante é sempre igual a zero. E a derivada de uma função do tipo , será:
Assim, para nossa função:
Teremos:
Então, podemos escrever a derivada de como sendo:
Ou melhor:
Passo 3
E aqui temos um problemas. Veja:
Para mostrar que não existe usaremos
E analisando as derivadas de cada lado, ficamos com. No lando esquerdo, temos:
E para o lando direito:
Como , então podemos dizer que não existe derivada de .
Para , ocorre a mesma conclusão. Assim, é derivável para todo ,exceto para e .
Passo 4
- Gráficos de e :
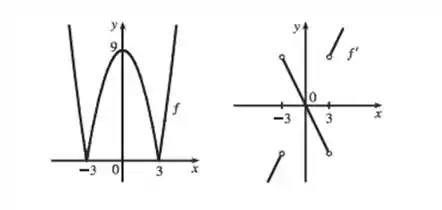
Veja que realmente há uma descontinuidade no gráfico de , mostrando que a derivada não existe nesses pontos.
Resposta
é derivável para todo ,exceto para e .