Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.7 - Ex. 51
(a) Verifique que a média das aproximações pela extremidade esquerda e pela extremidade direita dadas na Tabela 7.7.1 dá a Fórmula (2) da aproximação trapezoidal.
(b) Suponha que seja uma função contínua e não negativa no intervalo e subdivida em pontos igualmente espaçados Encontre a área do trapézio sob o segmento de reta que liga os pontos ( e acima do intervalo Mostre que o lado direito da Fórmula (2) é a soma dessas áreas de trapézios (Figura 7.7.1).
Passo 1
(a) Primeiro, vamos lembrar das fórmulinhas de aproximação pela extremidade esquerda e pela direita:
Pela esquerda:
Pela direita:
Precisamos provar que a média entre essas duas fórmulas dá:
Vem comigo!
Passo 2
Vamos calcular então:
Substituindo as fórmulas:
Colocando o termo em evidência e somando os termos de com índices iguais:
E essa é, realmente, a fórmula (2) da aproximação trapezoidal. Conseguimos!
Passo 3
(b) Queremos a área desse trapézio:
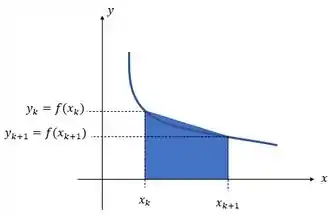
Só lembrarmos da fórmulinha de área do trapézio:
Olhando para a figura, vemos que nossa base maior tem de tamanho, enquanto a base menor vale e a altura do nosso trapézio é . A área fica assim, então:
Passo 4
Precisamos provar que a soma dessas áreas que estão dentro do intervalo , é igual ao lado direito da fórmula da aproximação trapezoidal.
Se a gente somar essas áreas de até , ficamos com:
Podemos reescrever o tamanho do subintervalo como:
Substituindo no somatório:
Passo 5
Calculando esse somatório a gente chega em:
Que é exatamente o lado direito da fórmula da aproximação trapezoidal.
Resposta
(a) Prova nos passos
(b) Prova nos passos