Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.8 - Ex. 44c
Em cada item, confirme o resultado com um CAS.
Passo 1
Tudo que a gente precisa fazer é jogar essa integral num CAS e ver se dá esse resultado mesmo.
A gente repara que essa integral é imprópria porque o integrando não está definido em .
Usando o Wolfram Mathematica, a gente vê que a integral dá:
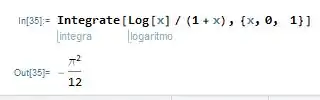
Deu igualzinho.
Se quisesse, poderia calcular essa integral no CAS numericamente e comparar com o valor de . Dá bom também!
Belezinha? Conseguimos!
Resposta
Confirmação nos passos
Exercícios de Livros Relacionados
Calcule: ∫ - ∞ + ∞ e - xd x
Determine k para que se tenha ∫ - ∞ + ∞ e k td t = 1
Calcule:int_1^(+ oo) (1)/(root(3)(x^4)) d x
Sejam alpha e s , s0 , reais dados. Verifique queint_0^(+ oo) e^(- s t) t e^(alpha t) d t = (1)/((s - alpha)^2) ( salpha )
Sejam dados um real s0 e um natural n ≠ 0 .Verifique que ∫ 0 + ∞ e - s tt nd t = n s ∫ 0 + ∞ t n - 1e - s td t Mostre que ∫ 0 + ∞ e - s tt nd t = n ! s n + 1