Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.7 - Ex. 37
Uma lata cilíndrica sem o topo é feita para receber de líquido. Encontre as dimensões que minimizarão o custo do metal para fazer a lata.
Passo 1
Fala aí. Tudo certinho com você?
Bom, essa questão pede pra gente encontrar as dimensões que minimizarão o custo com metal para a fabricação de uma lata cilíndrica sem a tampa feita para receber um volume .
Então a ideia aqui é pensar que a o metal será usado para a construção da superfície lateral e da base da lata. Sendo assim, precisaremos modelar o cálculo dessa superfície e encontrar as dimensões para que ela possua a menor área possível, mas tenha o maior volume.
Sendo:
E
Vamos otimizar essas relações. Vem que te mostro como.
Passo 2
Podemos começar esboçando o desenho da lata, como sendo:
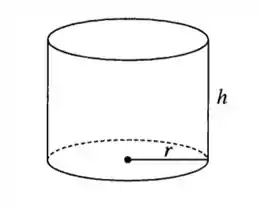
Como precisamos calcular as dimensões da superfície que nos trará o volume máximo do cilindro sem o topo, então temos a seguinte fórmula:
Dentro dessa lata precisamos conseguir colocar um volume , que tem por fórmula:
Com a fórmula do volume conseguimos isolar uma das variáveis para facilitar a nossa resolução e a vida:
Substituindo na fórmula da superfície do cilindro sem topo :
Que pode ser escrito com:
Passo 3
Como queremos o menor custo de material, precisamos minimizando . E fazemos isso encontrando sua derivada e igualando a zero.
Assim, como
Sua derivada em relação a será:
E igualdando a zero, teremos:
O que pode ser escrito com:
E isolando , temos:
Passo 4
Agora, substituindo em :
e em , temos:
E esse será o volume de nossa lata.
Resposta
Dimensões:
- Raio:
- Volume: