Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 22
Vimos, no exemplo 9, que a equação tem exatamente uma solução.
a) Use um gráfico para mostrar que a equação tem três soluções e encontre-as com duas casas decimais de precisão.
b) Encontre um valor aproximado tal que a equação tenha exatamente duas soluções.
Passo 1
Opa, bora lá! Temos a equação:
E a gente quer achar as três soluções dessa equação graficamente! Pra isso a gente vai se inspirar no exemplo dessa secção. Nele temos a equação:
E é plotada as curvas:
Assim o ponto de intersecção dessas duas curvas é a solução de . Beleza?!
Então aqui vamos plotar as curvas:
E procurar pelas intersecções.
Na letra (b) temos:
E queremos encontrar um valor aproximado para que a equação tenha exatamente duas soluções. Então vamos ter:
Pra isso a gente vai precisar "chutar" valores pra . Só que a gente vai fazer isso usando o bom senso! Se aumenta a inclinação da reta aumenta, se ele diminui a inclinação diminui...se ele fica negativo a reta passa a ser decrescente.
Então vamos olhar a reta da letra (a) e ver se ela nos dá uma luz pro melhor chute inicial!
Passo 2
Queremos achar as soluções da equação graficamente. Para isso, plotamos as funções e e olhamos para seus pontos de encontro:
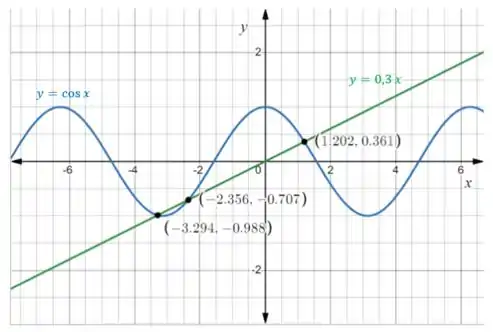
Assim, as soluções são:
Passo 3
Agora a gente precisa pensar no melhor . Sabemos que:
Tem soluções e:
Tem uma solução. Olhando pro gráfico acima dá pra perceber que se aumentarmos a inclinação da reta, então podemos chegar a um ponto com duas intersecções, mas se aumentarmos muito só vai ter uma intersecção, como em .
Ou seja, precisamos de um que seja maior que e menor que . Vamos testar :
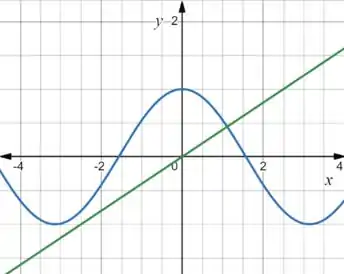
Ops, só uma intercepção. Então deve estar entre e . Vamos testar :
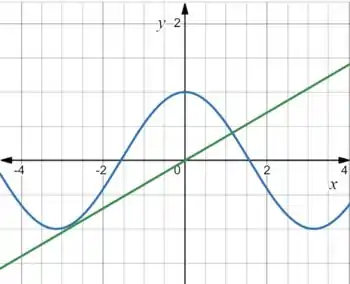
Quase lá! O tem que ser só um pouco menor que . Vamos testar :
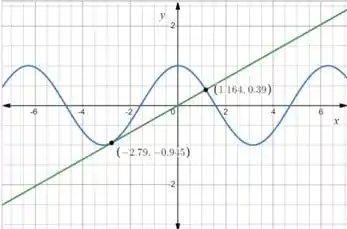
Perfeitoooo!
Temos então que:
Tem exatamente duas soluções!