Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 25
Para quais valores de é válido que ?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado quer saber para quais valores de é válida a expressão:
A forma mais fácil de descobrir isso seria plotando a curva e a reta horizontal em um gráfico e analisar os valores de que fazem ser menor que . Sacou?
Nós vamos analisar o intervalo em que a curva está abaixo da curva no gráfico para definir os valores que fazem nossa expressão ser válida.
Vamos lá!
Passo 2
Com o auxílio de um software, nós conseguimos plotar as duas funções que definimos no passo anterior:
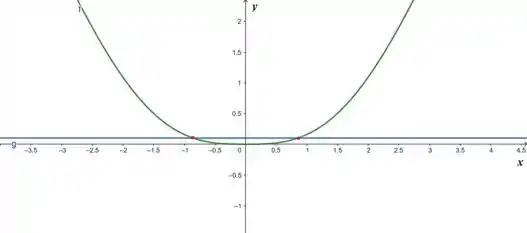
Repare que nós temos a curva em verde e a reta em azul. Os dois pontinhos vermelhos indicam os pontos de interseção dessas curvas, que acontecem em:
E
Observe que entre esses valores, a curva está sempre abaixo de . Dessa forma, podemos dizer que para qualquer dentro desse intervalo, , teremos:
E a nossa expressão será válida.
Valeu, galera! Até a próxima! 😉