Funções do 1º Grau
Produzido por Marcelo LuizTeoria
Introdução
Falaaa meus queridos, tudo certo!?
Nesse tópico vamos entender melhor o que é uma Função do 1º Grau e como ela se comporta graficamente.
Mas antes de falar disso precisamos nos fazer uma perguntar:
“O que é uma função?”
Na maioria das vezes, a primeira coisa que vem na nossa cabeça quando falamos de funções são aquelas notações comuns:
Mas o que realmente significa ser uma função?
Para responder isso vamos dizer que uma função “” é dada por .
Quando escrevemos queremos dizer que a função “” varia conforme o valor de “” também varia.
Ou seja, para , a função será:
Para :
E assim por diante...
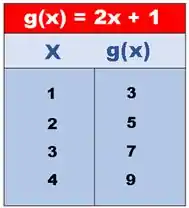
Percebeu? Conforme os valores de “” mudam, o valor da também muda, logo está em função de “”.
Função do 1º Grau ou Função Afim
Já demos uma relembrada nos conceitos de funções.
Mas como identificar uma função do 1º grau?
A lei de formação é dada por:
Onde:
coeficiente angular.
coeficiente linear.
Obs: é o mesmo que ,, ...
QUE??????

Relaaxa!!
Com um exemplo tudo fica mais fácil...
Olhe essa função:
Nesse caso:
;
;
.
Ok, mas pra que serve esses coeficientes?
Eles são importantes quando queremos estudar o comportamento gráfico das funções.
Gráfico da Função do 1º Grau
Grave isso:
“O gráfico de uma função afim sempre será um RETA!!!”
E agora, os valores de e de serão muito úteis para entendermos esses gráficos.
(coeficiente angular) – Será a inclinação da reta.
(coeficiente linear) – Será o valor em que a função cruza o eixo .
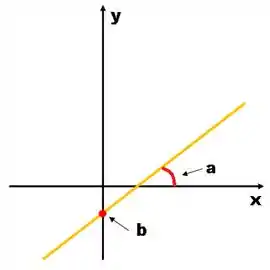
Mas como eu consigo montar um gráfico de uma função afim?
Como o gráfico da função afim é uma reta, basta que nós encontremos dois pontos por onde a reta passa e traçar a reta passando por eles.
Exemplo
Vamos esboçar o gráfico da função .
Primeiramente, precisamos achar dois pontos que pertençam à reta.
Esses pontos podem ser encontrados substituindo qualquer valor para , porém, para facilitar os cálculos, podemos escolher e .
Para , temos:
Para , temos:
Desse modo, encontramos dois pontos que pertencem à reta, dados pelos pares ordenados e :
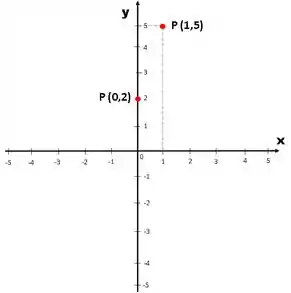
Por fim, como já temos dois pontos por onde a reta passa, precisamos apenas traça-la passando por esses dois pontos:
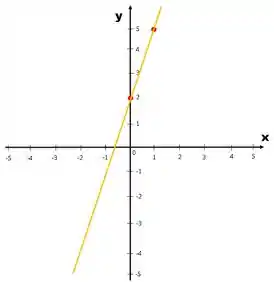
E está feito nosso gráfico da função .
Raiz de uma Função do 1º Grau
Em uma reta que se estende por todos os reais , o eixo terá em algum momento valor igual a zero.
Esse ponto ocorre graficamente quando a reta cruza o eixo .
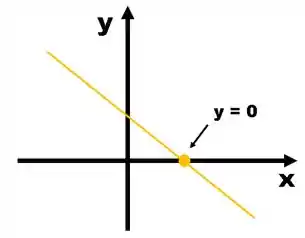
Mas como achar o valor da raiz?
Em uma reta , representa o eixo .
Dessa forma, se acharmos um valor de que faça com que , esse será a raiz da função.
Exemplo: Encontre a raiz da função
Primeiramente, igualamos a função a zero.
Agora é só resolver...
E está aí, a reta cruza o eixo em , logo, é a raiz da função.
Tranquilasso né!?
Função do 1º Grau ou Função Afim
Gráfico da Função do 1º Grau
Exemplo
Raiz de uma Função do 1º Grau
Exercícios Resolvidos
Exercício Resolvido #1
Autoria própria.
Determine o coeficiente linear da função .
Passo 1
Pela lei de formação, temos que:
Onde:
Coeficiente angular.
Coeficiente linear.
Sendo assim na função
Resposta
.
Exercício Resolvido #2
Autoria própria.
Encontre a raiz da função
Passo 1
Primeiramente, devemos igualar a equação a zero.
Resolvendo a equação, temos:
Resposta
.
Exercício Resolvido #3
Autoria própria.
Qual é o valor da função para .
a) 21
b) 17
c) 25
d) 23
e) 19
Passo 1
Tudo que precisamos fazer aqui é substituir o valor de na função.
Resposta
Alternativa d).
Exercício Resolvido #4
Autoria própria.
Determine a função afim , sabendo que e
Passo 1
Pelo enunciado, temos que , logo:
Também sabemos que , logo:
Como chegamos em duas equações com termos iguais, podemos montar um sistema.
Isolando na segunda equação, temos:
Passo 2
Substituindo o valor encontrado na primeira equação, conseguimos achar o valor de .
Como , o valor de também será igual a .
Com os valores de e conseguimos determinar a função.
Resposta
.
Exercício Resolvido #5
(U. Católica de Salvador-BA).
Seja a função de em definida por , determine o valor de .
Passo 1
Você pode encontrar esse resultado de duas maneiras.
1º Caso
Substituindo os valores em e depois subtraindo:
Passo 2
2º Caso
Podemos pensar que é uma unidade maior que .
Sendo assim, não importa quais valores pegarmos, desde que q tenham a mesma proporção.
Exemplo:
Para facilitar as contas podemos escolher e , e assim teremos:
Resposta
.
Exercício Resolvido #6
(U. F. Viçosa-MG).
Uma função é dada por , em que e são números reais. Se e , determine o valor de .
Passo 1
Para a função vale . Logo:
Para a função vale . Logo:
Como temos termos semelhantes, podemos montar um sistema de equações e descobrir os valores de e .
Isolando na segunda equação temos:
Substituindo na primeira equação, conseguimos encontrar o valor de .
CUIDADO COM O SINAL!!!
Substituindo o valor de na segunda equação, conseguimos achar o valo de .
Passo 2
Com os valores de e encontrados, podemos definir a função.
Para , temos:
Resposta
.
Exercício Resolvido #7
Elaboração Própria.
Esboce os seguintes gráficos:
Passo 1
a)
Para montar o gráfico de uma função afim, precisamos de 2 pontos para formar uma reta. Ou seja, escolhemos 2 valores para e descobrimos o valor de .
Note que , mas mesmo assim continuamos tendo uma função afim.
Vamos agora escolher dois valores de .
Para :
Para :
Assim, os pontos e pertencem a nossa reta:
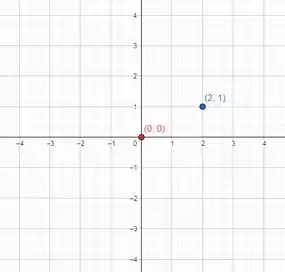
Agora é só traçar a reta que contém esses dois pontos:
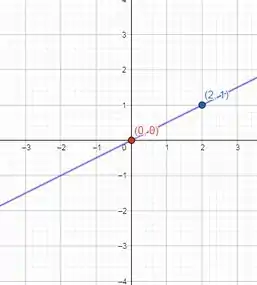
Pronto esse é o nosso gráfico.
Passo 2
b)
Novamente, vamos pegar dois valores de e calcularemos para esses valores:
Para :
Para :
Assim, temos os pontos e :
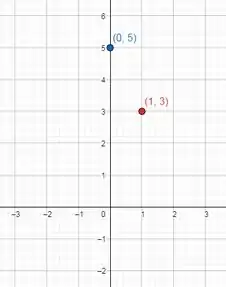
Agora, traçando a reta, temos que nosso gráfico é:
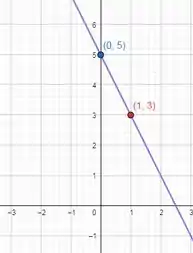
Resposta
a)
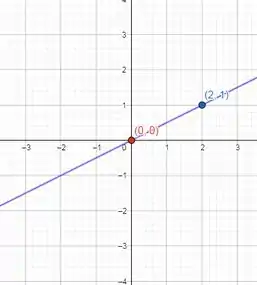
b)
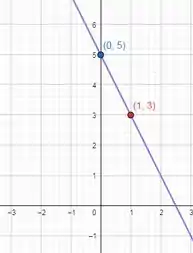
Exercício Resolvido #8
DANTE, Luiz Roberto. Matemática- contexto e aplicações. ED. Renovada. São Paulo, SP: ática, 2010. pp.121
Determine o valor de m para que os gráficos da função :
- Intersecte o eixo y no ponto ;
- Intersecte o eixo x no ponto ;
Passo 1
- Vamos relembrar que numa função afim, temos:
- Em um par ordenado, temos :
Na qual é o coeficiente linear, ou seja, o valor que intercepta o eixo y no nosso gráfico.
Nesse casso queremos que intercepte no valor
e
Assim queremos que
Na nossa funçãozinha temos :
Nosso coeficiente linear nesse caso é :
Assim, para que intercepte o eixo y
Passo 2
O primeiro valor corresponde ao valor de x e o segundo de y.
Feito isso, queremos:
O valor de e
Vamos substituir esse valor na nossa funçãozinha:
Lembrando que