Problemas com Funções do 1º Grau
Produzido por Marcelo LuizTeoria
Introdução
Anteriormente, vimos o que é e como se comporta uma função de 1º grau.
Mas será que essas funções são capazes de modelar situações do cotidiano?
Olhe esse exemplo:
Imagine que você precisa pegar um táxi do aeroporto até sua casa...

O preço da bandeira (valor inicial da corrida) é de reais e é cobrado reais a cada quilômetro percorrido.
O valor da bandeira nunca é alterado, porém a quantidade de quilômetros percorridos resultará no valor final da corrida.
Sendo assim, o valor da corrida varia conforme a distância varia. Podemos chamar a distância percorrida de e escrever a função:
Sendo,
O valor total da corrida.
A variável independente.
O valor da bandeira.
Montando o Gráfico
Atribuindo valores para podemos montar uma tabela e compreender melhor o comportamento dessa função:
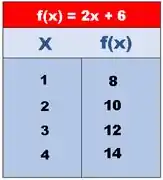
E o gráfico fica assim:
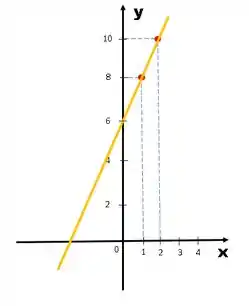
Equações do 1º Grau
O próximo passo depois de se familiarizar com as funções é estudar as equações.
Mas o que são equações do 1º grau e o que muda em relação às funções???
Nas funções o se comporta como uma variável independente, ou seja, conforme o valor de muda, o valor de também muda.
Já na equação, o irá se comportar como uma incógnita, ou seja, ela terá um valor específico para que não irá se alterar.
Vamos ver um exemplo...
Resolva a equação abaixo:
Deixando de um lado e números do outro teremos:
Nessa equação tem um valor específico .
Percebeu a diferença!?
Beleza... Mas por que as equações são tão importante para resolver problemas?
Em muitos casos, os problemas irão pedir um valor específico de e você só será capaz de encontrar a partir de uma equação.
Problema Prático
A diferença de idade entre dois meninos é de anos. Sabendo que o menino mais velho tem vezes a idade do mais novo, determine a idade atual dos dois meninos.
Vamos chamar a idade do menino mais velho de e a do mais novo de .
Sabemos que o menino mais velho tem idade igual a vezes a idade do menino mais novo
Também sabemos que a diferença de idade entre eles é de anos, logo:
Mas nó já sabemos que , então vamos substituir aqui
E está pronto nossa equação.
Resolvendo-a, poderemos encontrar a idade que o menino mais novo
Essa é a idade do mais novo! A idade do mais velho é 4 vezes isso, ou seja
Viu como as funções e as equações andam lado a lado nas resoluções desses problemas!?
Agora que já vimos como lidar e resolver esses problemas, que tal praticarmos um pouco?