Lei dos Senos e Lei dos Cossenos
Teoria
Introdução
Nesse texto, vamos falar de duas leis bem importantes no estudo da trigonometria e que vão nos ajudar na solução de diversos problemas. Vamos começar pela lei dos senos e depois caminhar para as leis dos cossenos.
Lei dos Senos
A lei dos senos não tem muito mistério, mas vamos dividi-la em duas partes para ficar mais fácil de entender o seu conceito. Imagine que temos um triângulo qualquer, pode ser qualquer triângulo mesmo.
Não, você não.
Pode ser isósceles, equilátero, retângulo ou qualquer outro rótulo, como abaixo:
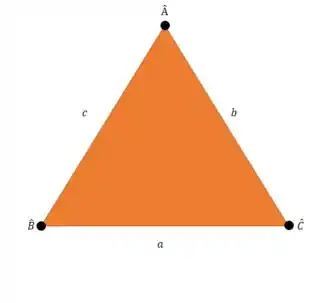
Temos um triângulo qualquer com ângulos e e os lados , e Veja que o lado é oposto ao ângulo , pois aponta para . O mesmo vale para que é o lado oposto ao ângulo e oposto a .
A primeira parte da lei dos senos diz que a razão entre um lado oposto e seu ângulo é sempre igual para todo o triângulo. Em outras palavras:
Até aí tudo bem? Sabemos que a razão entre um lado oposto e seu ângulo é sempre igual, mas qual o valor dessa razão? Essa é a motivação para a segunda parte da lei.
Para chegar nesse resultado, imagine que o triângulo está dentro de uma circunferência e todos seus vértices fazem parte desta circunferência, ou seja, tocam nela:
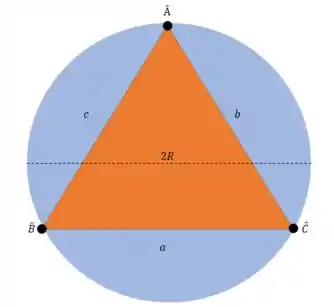
Quando isso acontece dizemos que o triângulo está inscrito na circunferência ou é um triângulo circunscrito. A razão entre o lado oposto e seu ângulo será sempre no triângulo e igual ao diâmetro, ou duas vezes o raio, de uma circunferência em que é possível inscrever o triângulo:
Se um triângulo tem ângulos , , com respectivos lados opostos , e e pode ser inscrito numa circunferência de raio , então:
Lei dos cossenos
Lembra do Teorema de Pitágoras, né? Ele diz que a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa. Esse Teorema é realmente muito bom e nos ajuda bastante quando temos dois lados de um triângulo retângulo e queremos achar o terceiro.
Repare, porém, que o triângulo tem que ser um triângulo retângulo. Mas e se precisarmos calcular o terceiro lado de um triângulo que não é retângulo? Aí jovem, entra a lei dos cossenos, que permite qualquer um terceiro lado de qualquer triângulo sabendo seu ângulo oposto e os outros dois.
Para ilustrar, observe o triângulo abaixo:
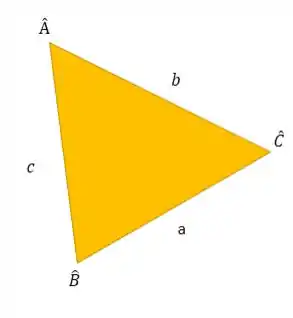
Se quisermos calcular conhecendo os outros lados e e o ângulo oposto , usamos a Lei dos Cossenos, que diz:
Ou seja, o quadrado de um lado de um triângulo qualquer é a soma do quadrado dos outros dois lados menos duas vezes o produto deles com o cosseno do ângulo oposto.
Repare que quando temos um triângulo retângulo, ainda podemos aplicar a lei dos cossenos.
Para a hipotenusa, teríamos:
Como o ângulo oposto a hipotenusa é e , tudo se resume a:
Que é o bom e velho Teorema de Pitágoras. Dessa maneira, o Teorema de Pitágoras passa a ser um caso particular da lei dos cossenos para quando o triângulo é um triângulo retângulo.
Conseguiu pegar? É importante nos acompanhar nos exercícios agora para colocar em prática tudo que foi visto. Vamos lá!
Lei dos cossenos
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Qual o valor de no triângulo abaixo.
Obs.: Se necessário, utilizar os valores de e .
Passo 1
Falaaaaa Galeeera!! Beleza?! Vamos ver como podemos encontrar o valor de no triângulo do enunciado??? Você tem algum palpite de como calcular???? Primeira coisa a se reparar é que o triângulo não é retângulo. É um triângulo qualquer.
Beleza... Então, se você reparar, nós temos o valor de ângulos do triângulo e estamos trabalhando com o valor de dois lados opostos a esses ângulos, concorda? Nesse caso, faz sentido pra gente utilizar a lei dos senos para resolver esse exercício!
Passo 2
A lei dos senos nos diz o seguinte
Onde e são os ângulos do trângulo e e os lados. Algo importante é que é o lado oposto ao ângulo . Da mesma forma, é o lado oposto ao ângulo .
Assim, substituindo os valores do triângulo, temos
Beleza?! Mas... e agora??
Agora podemos substituir os valores de e que foram dados no enunciado:
Passo 3
Multiplicando cruzado, temos
Fazendo as continhas,
Assim,
Show de bola?!
Resposta
Exercício Resolvido #2
Elaboração Própria
Calcule a medida do lado do triângulo abaixo:
Passo 1
Falaaaaa Aíí!! Vamos ver como podemos encontrar o valor de no triângulo do enunciado?? Primeira coisa que podemos reparar é que o triângulo não é retângulo. É um triângulo qualquer.
Beleza... Então, se você reparar, nós temos o valor de lados do triângulo e estamos trabalhando com o valor de um ângulo oposto a um desses lados, concorda? Nesse caso, faz sentido pra gente utilizar a lei dos cossenos para resolver esse exercício!
Passo 2
A lei dos cossenos nos diz o seguinte
Onde e são os lados do trângulo e o ângulo. Assim, substituindo os valores do triângulo, temos
Beleza?! Mas... e agora??
Agora precisamos lembrar o valor de . Para isso, basta olharmos para a tabelinha de ângulos notáveis:
Assim, substituindo o valor na equação, temos
Fazendo as continhas, temos
Ou seja,
Portanto,
Show de bola?!
Resposta
Exercício Resolvido #3
UF- Juiz de Fora
Dois lados de um triângulo medem e e formam um ângulo de . O terceiro lado desse triângulo mede:
Passo 1
Vamos lááááá!!! Geralmente, o melhor caminho para resolver exercícios que apresentam dois lados e um ângulo entre eles de um triângulo é a lei dos cossenos.
Beleza... Então, o lado oposto ao ângulo será e todos esses lados serão colocados na fórmula seguinte
Ahh, e são os lados que formam o ângulo.
Passo 2
Substituindo os valores na fórmula, temos
Fazendo as continhas,
Beleza?! Mas... e agora??
Agora precisamos lembrar o valor de . Para isso, basta olharmos para a tabelinha de ângulos notáveis:
Assim, substituindo o valor na equação, temos
Fazendo as continhas, temos
Ou seja,
Portanto,
Show de bola?!
Resposta
Exercício Resolvido #4
Elaboração Própria
O valor da medida do lado do triângulo abaixo vale:
- 10
- 20
- 30
- 40
- 50
Passo 1
Falaaaaa Aíí!! Vamos ver como podemos encontrar o valor de no triângulo do enunciado??
Primeira coisa que podemos reparar é que o triângulo não é retângulo. É um triângulo qualquer. Beleza... Então, se você reparar, nós temos o valor de lados do triângulo e estamos trabalhando com o valor de um ângulo oposto a um desses lados, concorda? Nesse caso, faz sentido pra gente utilizar a lei dos cossenos para resolver esse exercício!
Passo 2
A lei dos cossenos nos diz o seguinte
Onde e são os lados do trângulo e o ângulo. Assim, substituindo os valores do triângulo, temos
Beleza?! Mas... e agora??
Agora precisamos lembrar o valor de . Para isso, basta olharmos para a tabelinha de ângulos notáveis:
Assim, substituindo o valor na equação, temos
Fazendo as continhas, temos
Ou seja,
Portanto,
Show de bola?!
Resposta
Exercício Resolvido #5
UF- Juiz de Fora
Três ilhas , e aparecem num mapa em escala , como na figura. Das alternativas, a que melhor se aproxima de distância entre as ilhas e é:
Passo 1
Vamos lááááá!!! Geralmente, o melhor caminho para resolver exercícios que apresentam dois ângulos e um lado de um triângulo é a lei dos senos
A lei dos senos nos diz o seguinte
Onde e são os ângulos do trângulo e e os lados. Algo importante é que é o lado oposto ao ângulo . Da mesma forma, é o lado oposto ao ângulo .
Beleza?! Então vamos olhar para o nosso triângulo. Observe que o segmento é oposto ao ângulo . Pela soma das medidas internas de um triângulo, podemos concluir que o ângulo mede , show de bola?!
Os lados que serão usados nesse problema são e . Os ângulos opostos a esses lados são: e , respectivamente. Substituindo esses valores na lei dos senos, temos
Passo 2
Multiplicando cruzado, temos
Vamos agora olhar para a tabelinha dos ângulos notáveis para encontrar os valores dos acima
Assim, temos
Fazendo as continhas,
Terminamos??? Se você reparar não temos essa opção nas alternativas. Então, vamos substituir o valor da .
Portanto,
Passo 3
Terminamos??? NÃÃÃO!
O valor de que encontramos está em centímetros! Precisamos converter para Quilômetros! Assim,
Portanto, nossa resposta é a letra E!!
Resposta
Exercício Resolvido #6
UVA - Fernando Marinho - Lista 3 - 15
Uma construtora quer colocar uma ponte ligando os pontos e em lados diferentes de um rio. Os operários, estando em , precisam calcular a distância entre esses pontos. Dispunham apenas de um teodolito. Do ponto A. foram até o ponto , na mesma margem a quilômetros de distância. Os ângulos que obtiveram são e . Determine a distância entre e .
Passo 1
Bem, a primeira coisa a fazer é esboçar o problema. É formado um triângulo na seguinte forma:
Sendo que é o ângulo no vértice formado pelos lados compostos por e e é o ângulo no vértice formado pelos lados compostos por e .
Passo 2
Chamando o ângulo em de , Pela lei dos senos, temos que:
E queremos achar que é justamente a distância entre os pontos e . Não sabemos e , mas, como a soma dos ângulos de um triângulo é , concluímos que:
E:
Portanto:
Finalmente:
Resposta
Exercício Resolvido #7
Vestibular UNICAMP-SP
A água utilizada na casa de um sítio é captada e bombeada de um rio para uma caixa-d’água a de distância. A casa está a de distância da caixa-d’água e o ângulo formado entre as direções caixa-d’água-bomba e caixa-d’água-casa é de . Para bombear água do ponto de captação até a casa são necessários quantos metros de tubulação?
Passo 1
Novamente, vamos tentar esquematizar o problema desenhando o triângulo:
Passo 2
Temos dois lados de um triângulo e queremos achar o terceiro. Também temos o ângulo oposto, logo podemos aplicar a lei dos cossenos aqui:
Chamando a distância de , temos:
Agora é só substituir:
Logo:
Consideramos só a parte positiva da raiz porque trata-se de uma distância!
Resposta
Exercício Resolvido #8
Elaboração Própria
Na figura abaixo , , e . Qual a medida de ?
Passo 1
Nessa nem precisamos esquematizar o problema, já o temos em mão. Vamos ignorar as unidades por enquanto e visualizar o que importa:
Marcando isso tudo na figura:
Passo 2
A partir desses valores, podemos encontrar os outros. Veja que:
Logo:
Com esse ângulo, podemos usar a lei dos cossenos para achar :
Pelo círculo trigonométrico, tiramos que:
Assim:
Tendo raízes:
Mas a única que vale é a positiva, pois é uma medida.
Passo 3
Queremos chegar em , mas veja que o triângulo é retângulo, então podemos usar as relações trigonométricas sem medo. Considerando o ângulo de referência, é o cateto oposto e é a hipotenusa. Assim sendo, podemos usar o seno:
Relembrando a unidade: