Introdução à trigonometria
Teoria
Introdução
Vamos falar agora de trigonometria. O nome pode assustar um pouco, mas não tem nada demais. Basicamente, é o estudo das relações de um triângulo retangulo. Mas o que que eu tenho a ver com as relações desse cara?
Calma, calma. Além do triângulo retângulo ser importante por sí só, seu estudo ajuda a compreender outros fenômenos, como ondas, distâncias e circuferências. Então se ajeita na cadeira e vamos lá!
Relações trigonométricas
Vamos começar então. O triângulo retângulo é um triângulo que tem um dos ângulos igual a como o triângulo abaixo:
O ângulo representado pelo quadrado é o ângulo de e vai ser o nosso ângulo de análise. A partir dele, temos:
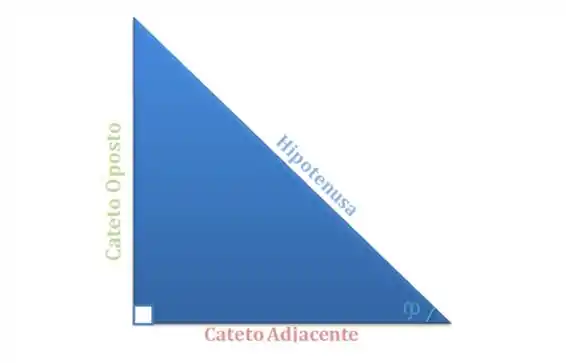
Onde cateto oposto é o lado para qual o ângulo de análise aponta.
Já o cateto adjacente é o lado que forma tanto o ângulo quanto o ângulo .
A hipotenusa, por sua vez, é a reta que liga o cateto oposto e o cateto adjacente. Para ficar mais bonito na hora representar algebricamente, vamos chamar o cateto oposto de , cateto adjacente de e a hipotenusa de mesmo.
Beleza? A partir disso, podemos definir:
Que pode ser lido como seno de , cosseno de e tangente de , sempre referido ao ângulo em questão.
Temos também que, associado a isso:
Que pode ser lido como cossecante de , secante de e cotangente de . Não vá pensar que a secante é sobre seno só porque começa com se hein?! A secante é sobre cosseno! (Dica: se ficar em dúvida, pensa na 3ᵃ letra da palavra: a 3ᵃ letra de secante é c, então é inverso do cosseno. A 3ᵃ letra de cossecante é s, então é o inverso do seno. )
Vamos prosseguir? Veja que:
Substituindo esses valores na tangente:
A mesma ideia segue para a cotangente também:
Opa! Vamos embalar agora. Lembra do Teorema de Pitágoras? Ele diz que:
Também substituindo:
Dividindo tudo por , chegamos na Relação Fundamental da Trigonometria:
Esse nome imponente não está aí a toa, essa relação é, de fato, muito importante. Lembre dela. Podemos também tirar outras relações a partir dela. Dividindo-a por :
Da mesma, maneira, se dividirmos tudo por , temos que:
Senos, cossenos e tangentes notáveis
O seno, cosseno e tangente não possuem uma relação linear, como veremos mais a frente. Isso significa que, por exemplo:
Para achar o seno de um ângulo você pode recorrer a boa e velha calculadora ou, quando ela não estiver disponível (julgo sempre quando você precisa) recorrer a uma tabelinha simpática de seno, cosseno e tangente de ângulos comuns nos problemas.
Como a calculadora é o Pokémon raro das provas, você precisa ter a tabelinha bem firme na cabeça! Lá vai:
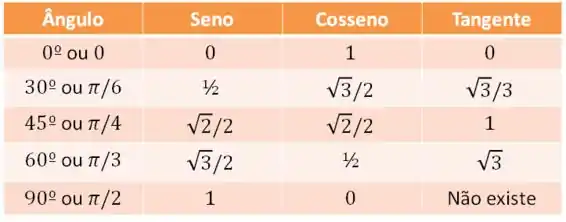
Se você não se lembra nem do que tomou hoje no café da manhã, não tem problema. Grave somente as colunas do seno e cosseno e lembre que a tangente é razão entre eles.
Se mesmo assim bater um branco e só lembrar de uma coluna, use a relação fundamental da trigometria para achar o resto.
Tudo bem? Nos vemos nos exercícios agora!
Senos, cossenos e tangentes notáveis
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Determine o valor do do ângulo do triângulo abaixo.
Passo 1
Fala Aíí!! Antes de qualquer coisa, vamos relembrar a definição de ?
O de um ângulo é calculado por
Beleza... mas quem é o Cateto Oposto e a Hipotenusa??
O Cateto Oposto é o lado do triângulo retângulo que está de frente pro ângulo que estamos analisando ,
Ou seja, o cateto Oposto aqui é a medida do lado . Beleza?! Podemos então já substituir esse valor na definição do:
Beleza... E quem é a Hipotenusa?? É o que vamos ver agora!!!
Passo 2
A Hipotenusa é a medida do lado do triângulo que está de frente para o ângulo de !
Ou seja, a nossa hipotenusa aqui vale a medida do lado ! Podemos então substituir esse valor na definição do :
Assim, o vale
Belezinha?!
Resposta
Exercício Resolvido #2
Elaboração Própria
Determine o valor do do ângulo do triângulo abaixo.
Passo 1
Fala Aíí!! Para resolver esse exercício, vamos relembrar a definição de ?
O de um ângulo é calculado por
E quem é o Cateto Adjacente e a Hipotenusa??
O Cateto Adjacente é a medida do lado do triângulo retângulo que não é a hipotenusa e forma o ângulo agudo.
Ou seja, o cateto Adjacente aqui é a medida do lado . Beleza?! Podemos então já substituir esse valor na definição do:
Beleza?!
Passo 2
Agora falta encontrar o valor da Hipotenusa!! A Hipotenusa é a medida do lado do triângulo que está de frente para o ângulo de !
Ou seja, a nossa hipotenusa aqui vale a medida do lado ! Podemos então substituir esse valor na definição do :
Assim, o vale
Belezinha?!
Resposta
Exercício Resolvido #3
Elaboração Própria
Determine o valor da do ângulo do triângulo abaixo.
Passo 1
Vamos Lá!!!! Vamos relembrar a definição da de um ângulo ?
A de um ângulo é calculada da seguinte maneira
E quem é o Cateto Oposto e Cateto Adjacente??
O Cateto Oposto é o lado do triângulo retângulo que está de frente pro ângulo que estamos analisando ,
Ou seja, o cateto Oposto aqui é a medida do lado . Beleza?! Podemos então substituir esse valor na definição de
Beleza?!
Passo 2
Já o Cateto Adjacente é a medida do lado do triângulo retângulo que não é a hipotenusa e forma o ângulo agudo.
Ou seja, o cateto Adjacente aqui é a medida do lado . Beleza?! Substituindo esse valor na definição de , temos
Show de bola?!
Resposta
Exercício Resolvido #4
Elaboração Própria
Calcule o valor de no triângulo abaixo:
Passo 1
Opaaa! Fala Aí!! Queremos encontrar o valor de , certo? Como podemos fazer isso???
Antes de mais nada, se você reparar, nós temos os valores de dois lados do triângulo retângulo e também temos o valor de um ângulo do triângulo . Certo?
Por isso, vamos utilizar uma das razões trigonométricas para encontrar o valor de ! Sempre que estivermos trabalhando com medidas dos lados de um triângulo retângulo e ângulo, podemos utilizar as razões trigonométricas para facilitar nossa vida!
Então como vai funcionar?????? É o que veremos agora!
Passo 2
Se observarmos bem o triângulo, nós temos um ângulo de e a medida que queremos encontrar está “de frente” para o ângulo de , concorda?
Ou seja, a medida é o cateto oposto ao ângulo de . Beleza?!
Além disso, temos a medida do lado que está de frente para o ângulo de , que é chamada de hipotenusa!
Como estamos trabalhando com a medida do cateto oposto e da hipotenusa , então a razão trigonométrica mais adequada que envolve o cateto oposto e a hipotenusa é o . Assim, precisamos calcular o !
Passo 3
Sabemos que o
Certo?! Aplicando essa fórmula para o , temos
Beleza?!
Passo 4
Tá... mas e agora?
Agora precisamos ver qual é o valor de . Para isso, basta olharmos para a nossa querida tabelinha!
Agora é só procurar o valor do
E substituir na nossa equação
E isolar o !!! Para isso, vamos multiplicar cruzado
Agora passamos o pro outro lado da igualdade dividindo
Assim,
Beleeeza?!
Resposta
Exercício Resolvido #5
Elaboração Própria
Uma bola é lançada sob um ângulo de . A que altura se encontra depois de percorrer em linha reta?
Passo 1
Falaaaaa Aí!! Antes de qualquer coisa vamos entender o que o exercício está pedindo?? No exercício é dito que uma bola é lançada sob um ângulo de . Ou seja,
Beleza?! Precisamos encontrar a altura que a bola vai se encontrar após percorrer em linha reta, ou seja
Queremos então encontrar o valor da altura !! Show de bola?!
Passo 2
Se observarmos bem o triângulo, nós temos um ângulo de e a medida que queremos encontrar está “de frente” para o ângulo de , concorda?
Ou seja, a medida é o cateto oposto ao ângulo de . Beleza?!
Além disso, temos a medida do lado que está de frente para o ângulo de , que é chamada de hipotenusa!
Como estamos trabalhando com a medida do cateto oposto e da hipotenusa , então a razão trigonométrica mais adequada que envolve o cateto oposto e a hipotenusa é o . Assim, precisamos calcular o !
Passo 3
Sabemos que o
Certo?! Aplicando essa fórmula para o , temos
Beleza?!
Passo 4
Agora precisamos ver qual é o valor de . Para isso, basta olharmos para a nossa querida tabelinha!
Agora é só procurar o valor do
E substituir na nossa equação
E isolar o !!! Para isso, vamos multiplicar cruzado
Agora passamos o pro outro lado da igualdade dividindo
Assim,
Ou seja, a altura que a bola se encontra depois de percorrer em linha reta é de !
Beleeeza?!
Resposta
A altura que a bola se encontra depois de percorrer em linha reta é de !
Exercício Resolvido #6
Unicamp-SP
Quando o Sol se encontra a acima do horizonte, um poste projeta sua sombra no chão com o comprimento de . Determine a altura do poste.
Passo 1
Vamos láá!! Vamos analisar e tentar esboçar o desenho do exercício?! No desenho abaixo, o segmento de reta amarelo representa um raio solar que é o responsável por originar a sombra do poste.
Se você reparar, temos o valor do ângulo de , o valor do comprimeto da sombra de e queremos encontrar o valor da altura . Beleza?!
Passo 2
Para calcularmos o valor da altura podemos utilizar a tangente
Onde o cateto oposto vale e o cateto Adjacente . Assim,
Beleza?!
Passo 3
Agora precisamos ver qual é o valor de . Para isso, basta olharmos para a nossa querida tabelinha!
Substituindo o valor da na nossa quação, ficamos com
Ou seja, a altua do poste é de
Beleza?!
Resposta
Exercício Resolvido #7
Unicamp-SP
Uma pessoa de 1,65 m de altura observa o topo de um edifício conforme o esquema abaixo.
Para sabermos a altura do prédio, devemos somar a:
Passo 1
Falaaaaa Galeeera!! Beleza?! Vamos analisar o desenho com um pouco mais de calma?? Vamos fazer um esboço mais simples para nos ajudar!
Se você reparar, o segmento que vale representa a altura da pessoa, certo?! Como o triângulo formado na imagem é retângulo, então o segmento CD também mede 1,65 metros. Beleza?!
Então vamos lá, se você reparar, o triângulo é retângulo. Perceba que a altura do prédio é igual a soma dos segmentos e . E como podemos encontrar o valor do segmento ?
É o que veremos agora!!
Passo 2
Para calcularmos o valor do segmento podemos utilizar uma das razões trigonométricas: ou . Lembrando que é a razão entre cateto oposto, ou seja:
O cateto oposto na nossa imagem é a medida do lado oposto ao ângulo , ou seja, . Já a hipotenusa é a medida do lado oposto ao ângulo de , ou seja, . Assim,
Isolando a altura que é o valor que queremos encontrar, temos
Essa é a nossa letra (e)!
Resposta
Letra E
Exercício Resolvido #8
UVA - Fernando Marinho - Lista 3 - 13
Uma escada de metros de comprimento está apoiada em uma parede, encostando num ponto a metros do chão. Qual é o ângulo de inclinação da escada em relação a parede?
Passo 1
A escada está para a parede formando um triângulo retângulo da seguinte forma:
Em relação ao ângulo , temos o cateto adjacente. Cateto adjacente e não oposto pois o está na parte de cima do triângulo. Além dele, temos a hipotenusa. Juntando os dois, podemos calcular o cosseno:
Passo 2
Para achar o ângulo, basta pensar: qual o ângulo cujo cosseno é ? Para responder a isso vamos usar a nossa querida tabelinha!
A resposta é e, portanto o ângulo será esse.
Resposta
Exercício Resolvido #9
[Temas Selectos /Lumbreras-Traduzido e Adaptado]
Fatore e simplifique a expressão:
.
Passo 1
Vamos usar aquele pulo do gato pra poder resolver! Isolando , teremos:
Passo 2
Da Relação Fundamental da Trigonometria, a gente sabe que:
Assim, teremos:
Opa, caímos na mesma relação de novo, agora é só correr pro abraço! Assim, vai sobrar...
Resposta
Exercício Resolvido #10
[Temas Selectos /Lumbreras-Traduzido]
Se , calcule .
Passo 1
Primeiro vamos relembrar o que é cossecante e cotangente! Temos que,
.
Assim, voltando à soma do enunciado, teremos:
O que nos dá:
Passo 2
Lá da Relação Fundamental da Trigonometria, temos que:
Isolando o , teremos:
Tacando lá na nossa equação, teremos:
Passo 3
Elevando ambos os lados ao quadrado, teremos:
Essa equação zera quando,
Ou
Maaaassssss... Como estamos interessados em calcular a . Então temos
Como a função seno está no meu denominador, eu não posso ter . Então vamos ficar com a nossa segunda solução
Calculando a cossecante, temos