Regra de 3 Composta
Produzido por Marcelo LuizTeoria
A regra de três composta nos permite resolver problemas matemáticos que envolvem mais de duas grandezas relacionadas entre si, direta ou inversamente.
-Que?! 😖
Olhe esse problema pra ficar mais claro:
Em
Temos
- Horas;
- Número de caminhões;
- Número de sacos de cimento;
Se problema apresenta três grandezas diferentes, não podemos usar a regra de 3 simples, ao invés disso, usamos a regra de 3 composta!
Como Fazer Regra de 3 composta - Passo a Passo
Pra a gente entender como calcular a regra de 3 composta, vamos pegar o exemplo que usamos ali em cima!
Em
Passo 1: Identificar a grandeza que contém a incógnita
A primeira coisa que vamos fazer é identificar qual é a grandeza que contém a incógnita, ela será o nosso produto. As demais grandezas envolvidas no problema serão nosso processo.
Beleza! A pergunta do enunciado é “quantos caminhões serão necessários para descarregar
Vamos organizar nossas informações:
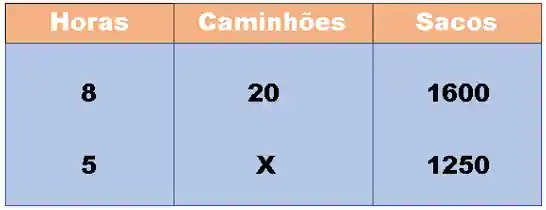
Passo 2: As grandezas são direta ou inversamente proporcionais?
Agora, relacionamos a grandeza que contém a incógnita com as duas outras:
- Quanto mais caminhões, mais sacos são descarregados. As grandezas são diretamente proporcionais, portanto, as setas possuem a mesma direção.
- Quanto mais horas, menos caminhões são necessários para concluir o trabalho. As grandezas são inversamente proporcionais, portanto, as setas possuem sentidos opostos.
Assim, temos:
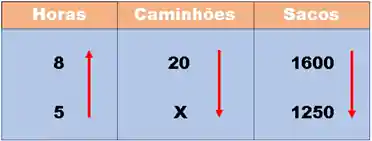
Passo 3: Montar a equação
Agora vamos montar a equação! Deixamos a grandeza que possui incógnita no primeiro membro da igualdade e depois o produto da galerinha que restou:
-Agora é só calcular o
Calma, ainda não!
Passo 4: Definir a ordem dos componentes
Caso a grandeza do processo seja inversa à grandeza do produto, inverta a ordem das componentes.
Nesse caso, como o número de horas é inversamente proporcional às outras duas grandezas, invertemos a ordem das componentes (colocamos
Passo 5: Calcular o
Até agora temos:
Isolamos o
Agora é só calcular:
E tá resolvido, para descarregar
Agora, vamos fazer um outro exercício?!
Exercício Resolvido
Se foram empregados
Regra de 3 Composta com 4 grandezas
-E se ao invés de
SIIM! 🤩 E digo mais, o passo a passo é igualzinho da regra de 3 composta pra 3 grandezas!
Vamos ver um exercício resolvido! 👇
Exercício Resolvido:
Uma fábrica automobilística com
Nossas grandezas são:
- Dias de trabalho;
- Número de Funcionários;
- Carga horária;
- Número de Peças
A pergunta é “Qual seria a produção em

Todos as grandezas são diretamente proporcionais. Isso é, quanto mais funcionários, mais horas por dia e mais dias, mais peças. Então teremos:
Que é a mesma coisa que fazer aquele x que fazemos em regra de 3 simples:

Isolando o
Ou seja, serão produzidas 647 peças!
Bora praticar com mais exercícios?!