Regra de 3 Simples
Teoria
Faaaaaaaaala meus queridos, tudo certo?
Já vimos o que são grandezas e como elas se relacionam entre si. Mas será que existe uma regra que nos ajuda no cálculo dessas grandezas???
Imagina que você vai fazer uma viagem de ida e volta para uma cidade, e na ida você vai com uma velocidade de e demora minutos pra chegar. Na volta, você quer chegar um pouquinho mais rápido, e decide ir com uma velocidade de . Quanto tempo você demoraria?
Será que existe alguma regra que nos ajuda a encontrar esse valor?
EXISTE SIM!!!
Essa regra é chamada de Regra de 3,ela basicamente resolve quase todos os problemas da humanidade, sério, não subestime o poder da regra de 3.
Tá, mas o que é essa regra de 3?
A regra de 3 é dividida em duas partes: Simples e Composta. Nesse tópico iremos focar na forma simples dessa regra e falar sobre as aplicações da maneira direta e inversa.
Onde usar a forma Direta?
Usamos a regra de 3 simples de forma Direta quando queremos calcular relações de grandezas do tipo: ”Quanto mais de uma coisa, mais de outra coisa”. Normalmente nos é dado 4 grandezas (3 grandezas conhecidas e uma incógnita) e queremos a partir dessa relação, descobrir quanto vale tal incógnita.
Veja esse exemplo:
Um veículo percorre em um tempo de em uma certa velocidade. Quantos segundos o mesmo veículo leva para percorrer ?
Aqui podemos ver um exemplo clássico de grandezas diretamente proporcionais, pois quanto mais o tempo passa, maior é o deslocamento do carro.
Nos casos em que temos a forma direta, tudo que precisamos fazer é multiplicar cruzado. Essa multiplicação nos dará uma equação do 1º grau.
Desse modo, teremos:
Tá aí. Rápido, fácil e sem stress!!!
Multiplicando cruzado e resolvendo a equação, encontramos o valor da incógnita e podemos dizer a partir da relação entre as grandezas que o veículo percorrerá em .
Outro exemplo:
Cinco caminhões transportam de areia, quantos caminhões são necessários para transportar de areia?
Nossas grandezas agora são :
- A quantidade de caminhões
- Volume de areia transportada
Podemos pensar:
Quanto mais caminhões tiverem, mais areia pode ser transportada. Ou seja, a medida que uma grandeza aumenta, a outra também aumenta, assim temos grandezas diretamente proporcionais.
Então temos:
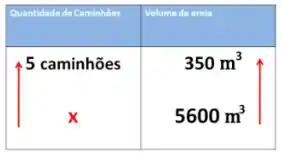
Agora, multiplicamos cruzado:
Ou seja, precisamos de caminhões.
Onde usar a forma Inversa?
Mas e quando a relação entre as grandezas é inversamente proporcional?
Para isso, usamos a forma inversa. Ela é bem parecida com a forma direta, porém, antes de multiplicar cruzado precisamos fazer inverter a ordem das grandezas.
Multiplicar cruzado? inverter a ordem das grandezas!?
Relaaaaaxa!! Vamos ver um exemplo clássico para ficar mais claro. Pense no seguinte problema:
Voltando ao problema do início, temos que:
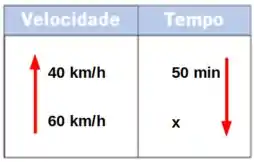
Um carro com velocidade percorre uma certa distância em um tempo . Qual será o tempo para concluir a mesma distância se o carro estiver a uma velocidade ?
Aplicação
Note que nesse caso, quanto uma das grandezas cresce, mais a outra grandeza diminui. Sendo assim, não podemos multiplicar cruzado. Precisamos inverter um dos lados das grandezas e só então multiplicar cruzado.
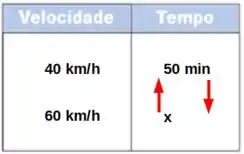
Ao inverter as grandezas podemos multiplicar cruzado e obter a equação assim como na forma direta.
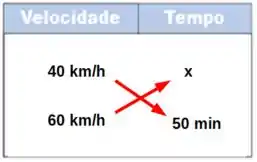
Logo, temos que:
Dessa forma, encontramos que nosso , ou seja, o carro leva menos tempo para percorrer uma certa distância se sua velocidade for maior. Temos então, um método para calcular as grandezas inversamente proporcionais.
Vamos pensar em outro exemplo
Duas pessoas pintam um muro em 10 dias, quantas pessoas terão que pintar esse mesmo muro para que seja em apenas 2 dias?
Agora, as nossas grandezas são quantidades de pessoas e tempo pra pintar um muro. Se aumentarmos o número de pessoas pintando, menor vai ser o número de dias para terminar. Quanto mais trabalhadores, menos tempo para fazer um determinado trabalho.
Ou seja, enquanto uma grandeza aumenta outra diminui, elas são indiretamente proporcionais.
Para resolver, vamos inverter umas das grandezas para podermos depois multiplicar cruzado:
Multiplicando cruzado :
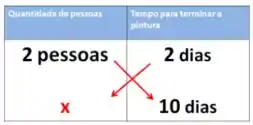
pessoas
E aí, bora praticar!?
Onde usar a forma Inversa?
Aplicação
Exercícios Resolvidos
Exercício Resolvido #1
Autoria própria.
Uma confeitaria recebeu um pedido de bolos para um grande evento que acontecerá na cidade. Sabendo que é gasto em média de farinha em cada bolo, qual será a quantidade total de farinha gasta para entregar os bolos que foram pedidos.
Passo 1
Primeiramente devemos identificar quais são as grandezas envolvidas no problema e determinar se são diretamente ou inversamente proporcionais.
O enunciado já nos apresenta quais são as grandezas envolvidas no problema, portanto, basta saber qual é a relação entre elas.
Como a quantidade de farinha aumenta conforme a quantidade de bolos aumenta, temos que as grandezas são diretamente proporcionais e então usaremos a regra de 3 de forma direta.
Passo 2
Para fazer bolo precisamos de de farinha. Para fazer bolos precisaremos de de farinha:
Assim, temos que:
Como o enunciado pediu o resultado em gramas, não precisamos fazer nenhuma conversão.
Resposta
.
Exercício Resolvido #2
Autoria própria.
Um pedreiro utilizou tijolos para construir três quartos de uma casa. Após fazer algumas mudanças na planta, o proprietário da casa sugeriu que fosse construído mais dois quartos com as mesmas dimensões.
a) Quantos tijolos a mais serão necessários para terminar a obra?
b) Quantos tijolos ao todo são necessários para terminar a obra?
Passo 1
O enunciado apresenta duas grandezas:
- Números de quartos.
- Quantidade de tijolos.
Quanto mais quartos são construídos, maior é a quantidade de tijolos utilizados. Portanto, é uma relação diretamente proporcional.
Passo 2
Letra a)
Com tijolos são construídos três quartos. Logo, para construir mais dois quartos será preciso tijolos
Devemos usar a regra de 3 de forma direta.
Multiplicando cruzado, temos:
Para a construção de mais dois quartos serão necessários tijolos a mais.
Passo 3
Letra b)
Já temos a quantidade de tijolos necessários para construir três quartos ( tijolos) e a quantidade necessária para construir dois quartos ( tijolos).
Agora é só somarmos as duas quantidades para obter a quantidade total para que a obra seja concluída.
Resposta
a) tijolos.
b) tijolos.
Exercício Resolvido #3
Autoria própria.
Mantendo um ritmo constante, um professor levou cerca de para corrigir redações.
a) Quantas redações ele corrigiu em ?
b) Quanto tempo ele levaria para corrigir redações?
Passo 1
Você concorda comigo que quanto mais redações tiverem, mais tempo o professor levará corrigindo? Então, quando um número aumenta, o outro também aumentar, por isso podemos dizer essas grandezas se relacionam de maneira diretamente proporcional.
Assim, podemos aplicar a regra de 3 de forma direta.
Passo 2
Letra a)
Em o professor corrigiu redações, portanto, em ele corrigiu redações.
Multiplicando cruzado, temos:
O professor corrigiu redações em hora.
Passo 3
Letra b)
Para corrigir redações o professor levou , portanto, para corrigir redações ele levará horas.
Multiplicando cruzado, temos:
O professor levará horas para corrigir redações.
Resposta
a) redações.
b) horas.
Exercício Resolvido #4
Autoria própria.
Uma pessoa tem uma dívida de reais no cartão de crédito, caso não quite a dívida, o acumulado da dívida no próximo mês será de reais. Considerando a mesma taxa de juros, quanto seria o acumulado de uma pessoa que possui uma dívida de reais?
Passo 1
Nesse exercício, a dívida inicial se relaciona diretamente com o aumento da dívida no próximo mês, porém, esse aumento não é dado de maneira direta, precisamos subtrair a dívida inicial da dívida final para saber qual foi o aumento
Com isso temos que o aumento na dívida foi de reais e podemos aplicar a regra de 3 de forma direta.
Passo 2
Com a dívida de reais o aumento será de reais. Logo, com a dívida de reais o aumento será de reais.
Aplicando a regra de 3, temos:
O valor do aumento seria de reais caso a dívida inicial fosse de reais.
Passo 3
Agora é só somarmos o valor da dívida inicial com o aumento:
Resposta
reais.
Exercício Resolvido #5
Autoria própria.
Uma empresa de tecelagem levou horas para produzir uma encomenda trabalhando em uma velocidade de metros de tecido por hora. Em quanto tempo a empresa concluiria o serviço caso a velocidade de produção fosse de metros de tecido por hora?
Passo 1
O tempo de conclusão do pedido está ligado com a velocidade de produção da empresa. Quanto mais rápido for a velocidade de produção, menor será o tempo de conclusão.
Dessa forma, temos que as grandezas são inversamente proporcionais.
Devemos aplicar a regra de 3 de forma inversa.
Passo 2
Com velocidade de a empresa leva para concluir o pedido, portanto, com velocidade de levará .
Invertendo um dos lados, temos:
Agora podemos multiplicar cruzado:
Portanto, se a velocidade for de o tempo de conclusão será de .
Resposta
horas.
Exercício Resolvido #6
Autoria própria.
Usando copos de , eu consigo servir um total de pessoas com uma quantidade fixa de suco. Quantas pessoas eu poderei servir se desta vez usar copos de ?
Passo 1
A quantidade de pessoas e o tamanho do copo (dado em ) são as duas grandezas envolvidas nesse problema.
Quanto maior for o copo, menos pessoas sou capaz de servir, uma vez que a quantidade de suco não muda. Portanto, as grandezas são inversamente proporcionas.
Sendo assim devemos usar a regra de 3 de maneira inversa.
Passo 2
Com copos de servimos pessoas, logo, com copos de , serviremos X pessoas.
Temos que:
Como trata-se de uma regra de 3 inversa, devemos inverter um dos lados da equação:
Passo 3
Agora podemos multiplicar cruzado e resolver a equação:
Então, com copos de eu poderei servir pessoas apenas.
Resposta
.
Exercício Resolvido #7
Autoria própria.
Uma caixa d’água é enchida em com torneiras abertas simultaneamente. Quanto tempo será preciso para encher o mesmo tanque se apenas duas torneiras estiverem abertas? O resultado final é dado em horas.
Passo 1
Primeiramente, identificamos as grandezas envolvidas no problema:
- Número de Torneiras.
- Tempo para encher a caixa d’água.
Quanto menos torneiras temos, maior será o tempo para encher a caixa. Sendo assim, as grandezas são inversamente proporcionais.
Devemos aplicar a regra de três de maneira inversa.
Passo 2
Com torneiras enchemos a caixa em , logo, com torneiras, encheremos a caixa em .
Como as grandezas são inversas, invertemos um dos lados da equação:
Passo 3
Agora podemos multiplicar cruzado e resolver a equação para encontrar o valor de :
Desse modo achamos que .
Passo 4
Precisamos agora passar o resultado para horas.
Como equivale à , basta dividir o resultado encontrado em minutos por .
Que equivalem a 1h e 15 min, beleza?
Resposta
horas.
Exercício Resolvido #8
Autoria própria.
Um funcionário de estoque costuma empilhar as caixas de ferramenta sempre da mesma maneira, ele organiza de modo que se forma colunas com caixas em cada coluna. Visando economizar espaço, ele mudou o layout deixando agora apenas colunas. Quantas caixas irão ficar em cada coluna nesse novo layout?
Passo 1
Como o número de caixas não muda, temos que quanto mais colunas forem feitas, menor será o número de caixas em cada uma.
Portanto as grandezas são inversamente proporcionais.
Devemos aplicas a regra de três de forma inversa.
Passo 2
Temos que para colunas são colocadas caixas em cada coluna, então, para colunas, colocamos caixas por coluna:
Como as grandezas são inversamente proporcionais, invertemos um dos lados da equação:
Passo 3
Agora podemos multiplicar cruzado e resolver a equação:
Devemos então empilhar caixas em cada uma das colunas.
Resposta
.