Soma e Subtração de Frações
Produzido por Marcelo LuizTeoria
Bora tirar todas as dúvidas sobre Soma e Subtração de Frações?!
Como Somar e Subtrair de Frações com Denominadores Iguais
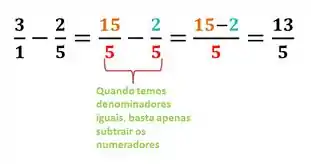
Bora começar com o caso mais fácil de todos! Quando a gente tem uma soma, ou subtração de frações com o denominador igual. Dá só uma olhada nesse exemplo:
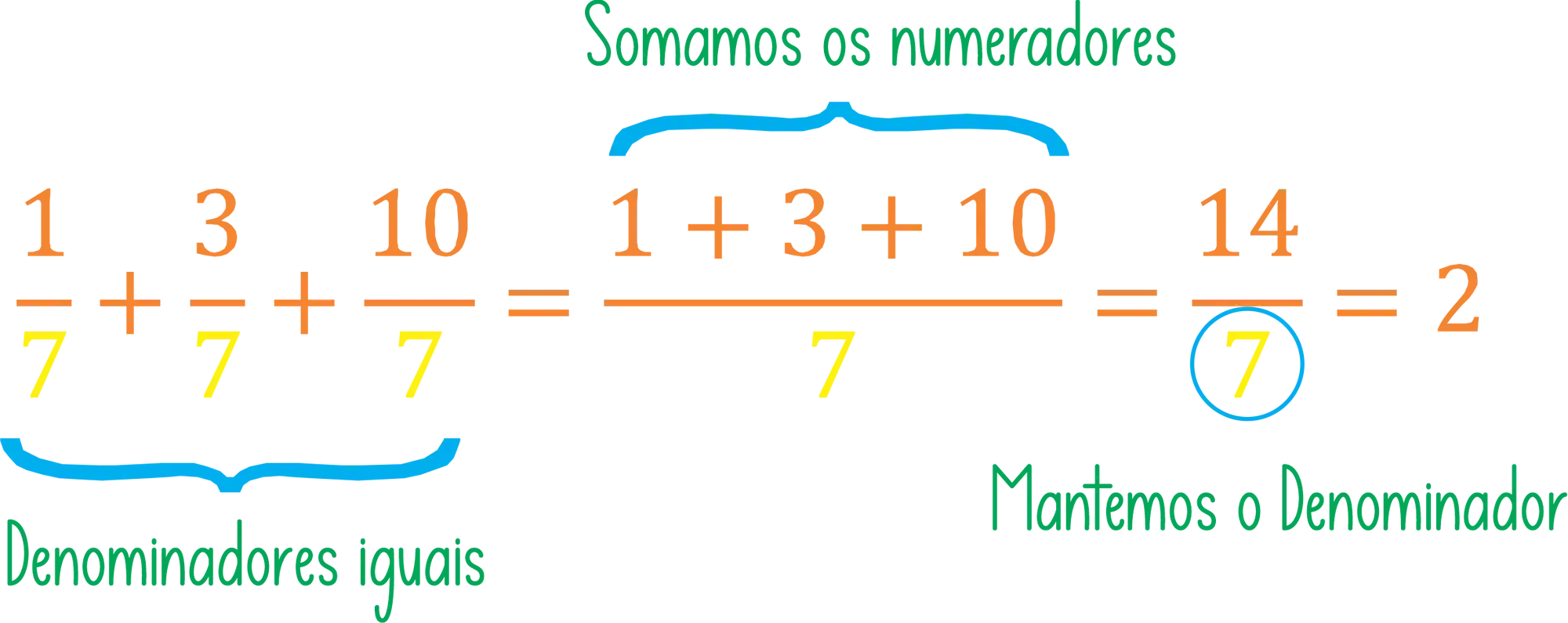
Acima podemos ver uma soma de frações com o mesmo denominador, nesse caso tudo o que temos que fazer é somar os numeradores e manter o denominador! E no caso da subtração a lógica é a mesma, subtraímos os numeradores e mantemos o denominador.
Molezinha, né? Agora podemos passar de nível! 🤣
📢 Clique para ver mais:
Como Somar e Subtrair de Frações com Denominadores Diferentes
Agora, como você faria essa subtração aqui:
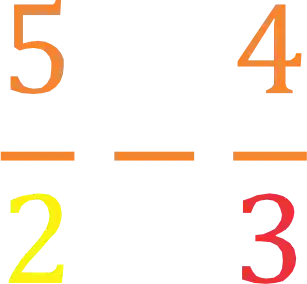
Passo 1: M.M.C.
Pra resolver esse problema, primeiro precisamos fazer um M.M.C entre os denominadores:
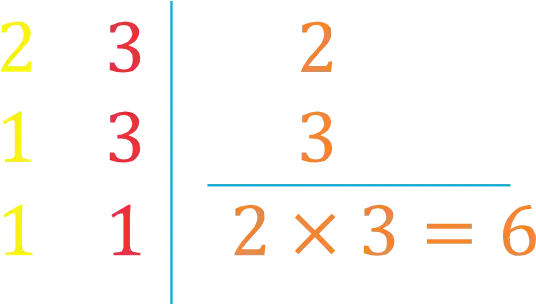
Passo 2: Calculamos os Novos Numeradores
O resultado do passo anterior vai ser o denominador da resposta final, mas agora precisamos saber quem vão ser os denominadores!
Para isso vamos pegar o
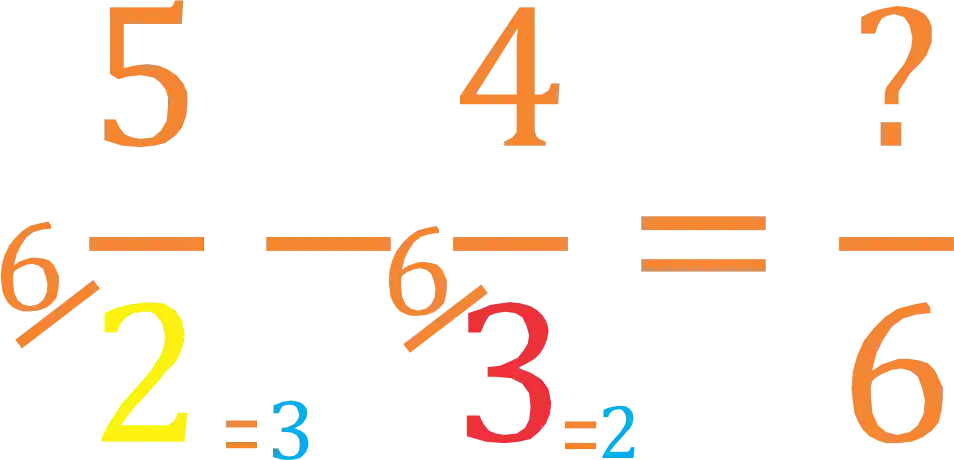
Depois disso, pegamos cada resultado e multiplicamos pelo respectivo denominador, assim:
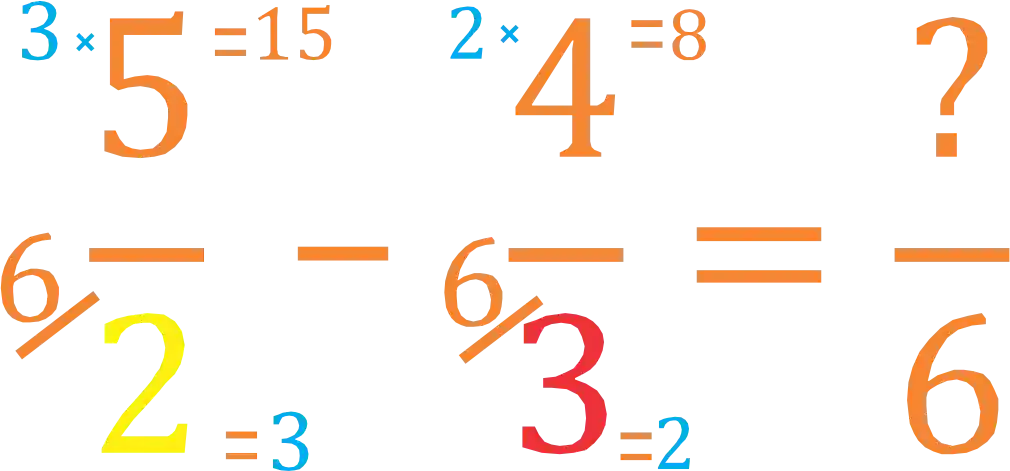
Esses serão os novos denominadores!
Passo 3: Calculamos as Frações
Agora a gente só precisa somar os numeradores e manter o denominador!
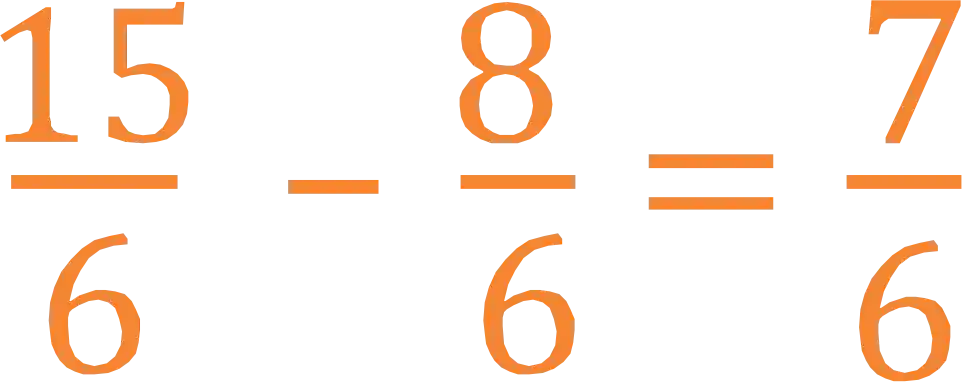
Prontinho!
Como Somar e Subtrair de Frações e Números Inteiros
E agora pra encerrar, como você faria essa continha aqui:
Temos um número inteiro e uma fração, então como proceder?!
Aqui vale lembrar, que todo número inteiro pode ser representado como uma fração basta apenas colocarmos o número 1 no denominador:
Feito isso, agora é só fazer a mesma conta para somarmos ou subtraímos frações com denominadores diferentes.
Agora, vamos praticar com exercícios?
Como Somar e Subtrair de Frações e Números Inteiros
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Encontre o MMC entre
, ,
Passo 1
Vamos colocar os números um do lado do outro e uma reta
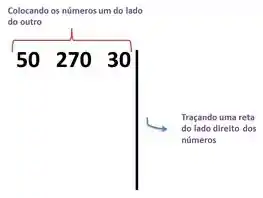
Passo 2
Na direita você vai dividir pelo menor número primo ( 2, 3, 4,5 ...) múltiplo dos números que estão á esquerda ( se o não houver divisão exata, você simplesmente repete o número).
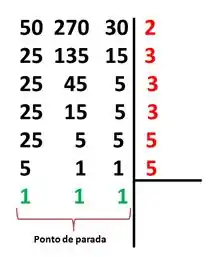
Passo 3
Para descobrirmos o MMC, basta multiplicarmos os valores que temos do lado direito.
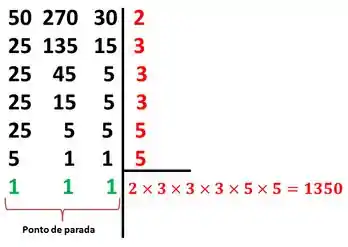
Resposta
1350
Exercício Resolvido #2
Elaboração própria
Encontre a fração irredutível :
Passo 1
Para encontarmos a fração irredutível, precisamos simplificar a fração, ou seja dividir o numerador e multiplicador, por um número múltiplo comum entre ambos.
Passo 2
- Podemos começar simplificando por 3
Novamente conseguimos simplificar por 3:
Não conseguimos simplificar mais, logo é a fração irredutível.
Passo 3
- Podemos começar simplificando por 2
Novamente, simplificando por 2:
Não conseguimos simplificar mais, logo é a fração irredutível.
Resposta
Exercício Resolvido #3
Elaboração própria
Faça a subtração
Passo 1
Lembrando que:
Basta resolvermos:
Passo 2
- Vamos calcular o MMC dos denominadores 1 e 5:
- Vamos pegar o valor do MMC, dividir pelo denominador de cada uma das frações (uma de cada vez) e multiplicar pelo valor do numerador.
- Subtraindo:
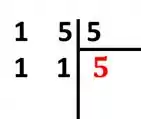
Passo 3
Para a primeira fração:
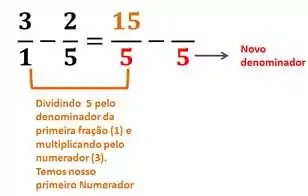
Para a segunda fração:
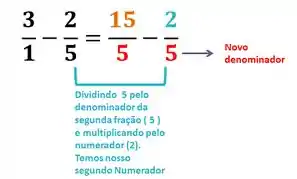
Passo 4
Resposta
Exercício Resolvido #4
Elaboração própria
Resolva:
Passo 1
- Vamos encontrar o MMC dos denominadores :
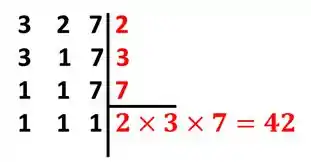
Passo 2
- Vamos pegar o valor do MMC, dividir pelo denominador de cada uma das frações (uma de cada vez) e multiplicar pelo valor do numerador.
Para a primeira fração:
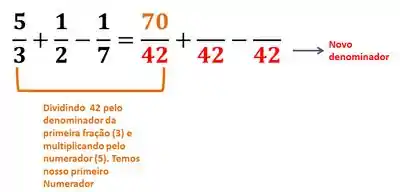
Para a segunda fração:
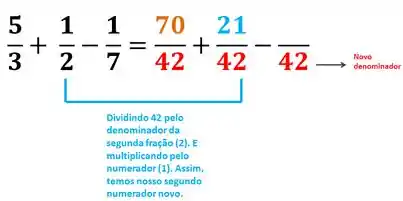
Para a última fração :
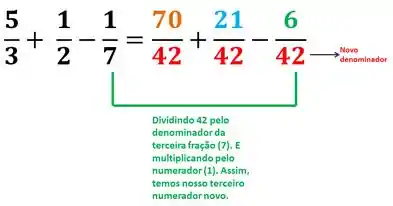
Passo 3
Prontinho agora é so resolver essa expressão:
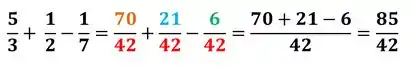
Resposta
Exercício Resolvido #5
GIOVANNI JR, José Ruy; CASTRUCCI, Benedicto. A conquista da Matemática 6º Ano. ED. Renovada. São Paulo, SP: FTD, 2009. pp.174
O mês de Setembro tem 30 dias. Já se passaram do número de dias do mês. Quantos dias ainda faltam para terminar o mês de setembro?
Passo 1
Vamos relembrar que a fração é uma parte de um todo, aonde o todo é dividido em partes iguais.
Quando temos uma fração, o denominador sempre vai ser a quantidade de partes iguais na qual dividimos (ou repartimos) o todo e o numerador vai ser o quanto foi usado dessas partes.
Nesse caso 30 dias representa o total (ou o todo) de dias do nosso mês. A fração mostra que você repartiu esses 30 dias em 10 partes iguais.
Assim, precisamos saber quantos dias têm em cada uma dessas partes.
Pra isso é só pegar os 30 dias e dividir em 10 partes, ou seja:
Isso mostra que o mês de setembro foi dividido em 10 grupos, cada um com três dias.
Passo 2
O enunciado também fala que já se passaram (ou que foi usado) 7 partes das 10, sabendo que cada uma das partes possui 3 dias, temos:
Assim já se passaram 21 dias de setembro!
Passo 3
Agora falta descobrir quantos dias faltam para acabar o mês, sabemos que ele tem 30 dias e já se passaram 21, logo faltam:
9 dias para o mês acabar
Resposta
9 dias
Exercício Resolvido #6
GIOVANNI JR, José Ruy; CASTRUCCI, Benedicto. A conquista da Matemática 6º Ano. ED. Renovada. São Paulo, SP: FTD, 2009. pp.190
Todos os 9 capítulos do livro que estou lendo têm a mesma quantidade de páginas. Sabendo que eu já li 5 capítulos, responda:
- Que fração do livro eu já li?
- Que fração do livro falta para eu terminar a leitura?
Passo 1
- O nosso todo é o livro inteiro, e ele foi dividido em 9 capítulos iguais, logo esse vai ser o denominador da nossa fração. E desses já lemos 5 capítulos.
- Para que termine o livro, você precisa ler os 9 capítulos, ou seja, o livro completo é representado por:
Assim, já lemos:
Do livro.
Passo 2
E você já leu do livro, por isso faltam para terminar:
Como são denominadores iguais, vamos manter o denominador e subtrair os numeradores:
Assim faltam quatro nonos do livro para terminar
Resposta
Exercício Resolvido #7
Ribeiro, Jackson; Matemática 6º Ano- Projeto RADIX . São Paulo, SP: Scipione, 2009. pp.135
O tanque de combustível de um veículo estava vazio e foi abastecido com de sua capacidade de álcool e de gasolina.
- Com que fração da capacidade do tanque o veículo foi abastecido?
- Que fração da capacidade do tanque faltou para que ele ficasse cheio?
Passo 1
- O tanque vazio foi abastecido com de álcool e de gasolina, assim o total que foi abastecido é de:
- Sabemos que já usamos do tanque. Para enchê-lo completamente precisaríamos de . Pra descobrir o quanto falta:
Para resolver essa soma, vamos encontrar o mmc dos denominadores 3 e 5:
1º Passo: Vamos colocar os números (3 e 5) um do lado do outro e fazer uma reta á direita deles, depois é só ir escolhendo números primos que divida pelo menos um dos números do lado esquerdo e fazer a divisão pelo primo escolhido.
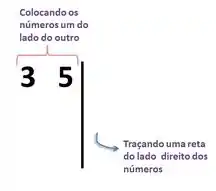
Vamos escolher o numero primo 3, por que conseguimos dividir o número 3 que temos na esquerda. Feito a divisão vamos só repetir embaixo. Como não é exato, vamos apenas repetir o 5.

Escolhendo outro primo.
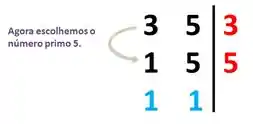
2º Passo: Para descobrirmos o MMC, basta multiplicarmos os valores que temos do lado direito.
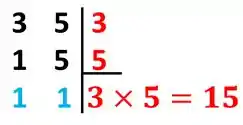
Logo o mmc entre 3 e 5 é 15
Agora, vamos pegar o valor do MMC, dividir pelo denominador de cada uma das frações (uma de cada vez) e multiplicar pelo valor do numerador.
Para a primeira fração:
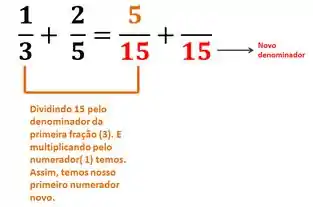
Para a segunda fração:
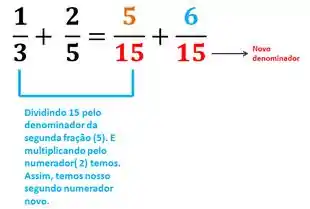
Prontinho, agora é só somar:
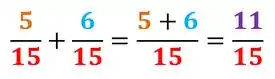
Assim, o veículo foi abastecido com da sua capacidade total.
Passo 2
Como os denominadores são iguais, vamos subtrair os numeradores e manter o denominador.
Logo, temos que completar da sua capacidade para que o tanque fique cheio.
Resposta
Exercício Resolvido #8
Ribeiro, Jackson; Matemática 6º Ano- Projeto RADIX . São Paulo, SP: Scipione, 2009. pp.119 (Adaptado)
Uma pessoa adulta dorme cerca de do dia. Quantos dias são necessários para que uma pessoa adulta durma equivalente a:
- Um dia inteiro
- Dois dias inteiros
Passo 1
- Uma fração é uma parte de um todo, aonde o todo é dividido em partes iguais.
- Se a pessoa consegue dormir equivalente a um dia , em 3 dias. Para a descobrirmos o equivalente a 2 dias é só:
Nesse caso 24 representa o total (ou o todo) de horas do nosso dia.
Uma pessoa dorme do dia. Para descobrirmos quanto isso vale em horas, vamos pensar no seguinte :
O dia foi dividido em três partes iguais, logo se pegarmos às 24 horas e dividirmos por três vamos descobrir quantas horas ela dorme por dia. Assim :
Já descobrimos, então, que uma pessoa dorme 8 horas por dia. Como cada dia tem 24 horas, para que ela consiga dormir o total de um dia, ela precisa :
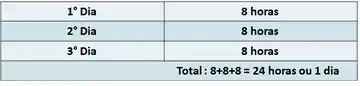
Ou seja, com 3 dias ela consegue dormir equivalente há um dia inteiro.
Passo 2
Resposta
- 3
- 6