Teorema de Pitágoras
Produzido por Marcelo LuizTeoria
Um dos principais assuntos quando falamos sobre triângulos é o Teorema de Pitágoras.
Mas pra que será que serve esse teorema??
Veja o triângulo abaixo:
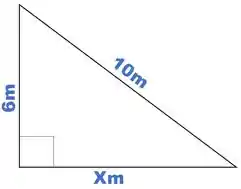
Com Pitágoras somos capazes de encontrar o valor de com apenas uma fórmula simples.
Mas se liga!!!
Para que sua aplicação seja possível, é necessário que haja um triângulo retângulo, que como vimos anteriormente, é aquele que tem um de seus ângulos internos igual a
Introdução
Para você que adora uma definição, segura essa aí:
Definição: Em um triângulo retângulo, temos que a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
CATETO? HIPOTENUSA?? QUEEEE??

Ok... Isso pode assustar um pouco de cara, mas respira fundo e vem comigo...
Vamos entender primeiro o que é essa tal de hipotenusa e o que são esses catetos.
Em um triângulo retângulo, os catetos sempre serão os lados encostados no ângulo reto e a hipotenusa sempre estará oposta ao ângulo reto.
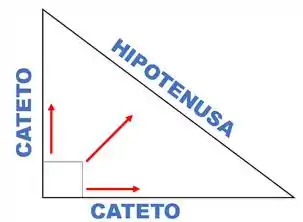
Por conveniência, podemos dizer que:
- Hipotenusa .
- Cateto .
- Outro Cateto .
Dessa forma chegamos na fórmula do Teorema de Pitágoras:
Relações importantes
Já vimos que o Teorema de Pitágoras só pode ser aplicado em triângulos retângulo. Mas será que tem algum jeito de aplicar nos outros tipos de triângulos também?
SIM!!! E é por isso que Pitágoras é tão importante quando falamos de triângulos...
Olhe o triângulo abaixo:
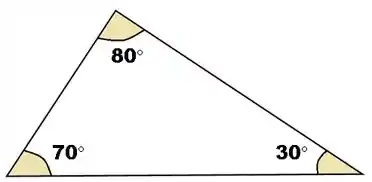
A princípio não sabemos aplicar Pitágoras, pois não temos um triângulo retângulo.
Em casos como esse, colocamos uma reta que liga um dos vértices até o lado oposto.
Ao fazermos isso, teremos dois triângulos retângulos e assim, seremos capazes de aplicar Pitágoras em cada um deles.
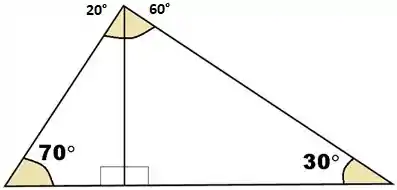
Pronto, desse modo conseguimos separar um triângulo inicial em dois triângulos retângulos e assim podemos aplicar Pitágoras para encontrar a medida de seus lados.
Aplicação
Que tal a gente ver como isso funcionaria na prática agora?
Determine a medida do lado não conhecido do triângulo abaixo:
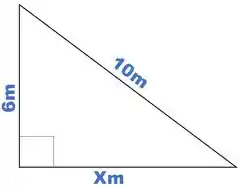
Pela fórmula sabemos que hipotenusa ao quadrado é igual à soma dos catetos ao quadrado.
Beleza, mas quem é a hipotenusa?
Moleza, é só lembrar da regrinha que diz que a hipotenusa é oposta ao ângulo de .
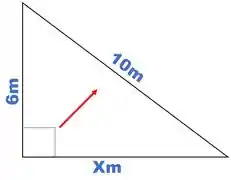
Agora que já encontramos quem é a hipotenusa, podemos colocar tudo na fórmula, desse modo, teremos que:
“Tcharaaaam”
Está resolvido, pelo Teorema de Pitágoras fomos capazes de encontrar que a medida do lado restante vale metros.
Ficha de Resumo
Recapitulando...
1º - Aplicamos o Teorema de Pitágoras exclusivamente em triângulos retângulos.
2º - Os catetos são adjacentes ao ângulo de (colados ao ângulo de ).
3º - A hipotenusa é sempre oposta ao ângulo de .
4º - Podemos traçar uma linha ligando um dos vértices à margem oposta, formando assim, dois triângulos retângulos.
5º - Fórmula do Teorema de Pitágoras é dada por:
Os exercícios envolvendo Pitágoras serão em geral, variações do exemplo que nós fizemos.
Portanto, para ficarmos craques basta treinar bastante até que a ideia seja fixada na nossa cabeça.
Bora praticar?
Relações importantes
Aplicação
Ficha de Resumo
Exercícios Resolvidos
Exercício Resolvido #1
Autoria própria.
Um jato percorre metros inclinadamente, e atinge uma altura de metros. Qual é a distância que o jato percorreu horizontalmente em relação ao plano horizontal do solo?
Passo 1
A trajetória inclina e a altura do triângulo podem ser descritas como um triângulo retângulo
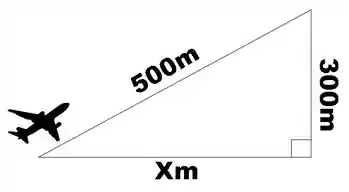
Com isso podemos aplicar o Teorema de Pitágoras para achar o valor de :
Agora é só tirar a raiz quadrada para saber o valor de
Resposta
metros.
Exercício Resolvido #2
Autoria própria.
Um campo de futebol retangular tem comprimento igual a metros e largura de metros. Qual a distância percorrida por um jogador que cruza de uma ponta a oura diagonalmente.
Passo 1
A trajetória do jogador dividi o retângulo em dois triângulos retângulos.
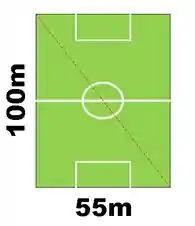
Dessa forma, a trajetória do jogador será a hipotenusa e os lados do campo os catetos.
Podemos, portanto, aplicar Pitágoras para descobrir o a distância percorrida pelo jogador:
Resposta
metros.
Exercício Resolvido #3
Autoria própria.
Um homem encosta a ponta de uma barra de ferro em um muro de metros, deixando a barra na diagonal. Sabendo que a distância da base do muro até a base da barra é de metros, determine o comprimento da barra.
Passo 1
Com as informações dadas podemos montar o triângulo abaixo:
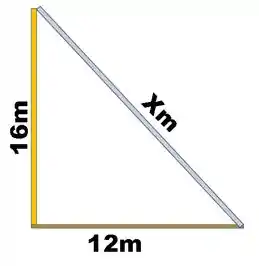
Como temos um triângulo retângulo podemos aplicar Pitágoras, sendo (barra de ferro) a hipotenusa.
Tirando a raiz quadrada, teremos o comprimento da barra:
Resposta
metros.
Exercício Resolvido #4
Autoria própria.
Um homem deseja cercar seu terreno na forma de um triângulo retângulo com um muro. O maior lado do triângulo que mede metros está encostado em um riacho e, portanto, não precisa ser cercado. Quantos metros de muro deverão ser construídos sabendo que o menor lado mede metros?
Passo 1
Primeiramente, devemos aplicar o teorema de Pitágoras para descobrir o valor do lado restante.
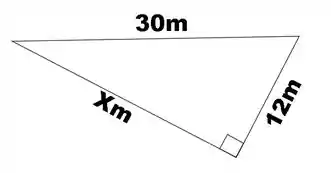
Passo 2
Agora precisamos encontrar o perímetro do triângulo:
O comprimento total do muro será o perímetro do triângulo menos o lado encostado no riacho:
Resposta
metros.
Exercício Resolvido #5
(CFT-MG).
As extremidades de um fio de antena totalmente esticado estão presas no topo de um prédio e no topo de um poste, respectivamente, de 16 e 4 m de altura. Considerando-se o terreno horizontal e sabendo-se que a distância entre o prédio e o poste é de 9 m, o comprimento do fio, em metros, é
a) 30 m
b) 15 m
c) 26 m
d) 35 m
e) 42 m
Passo 1
O fio está ligado do alto do prédio ao topo do fio.
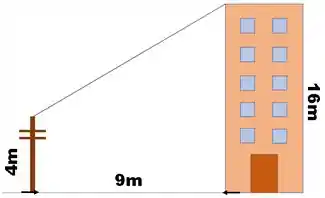
Podemos tomar o comprimento do fio como a hipotenusa de um triângulo formada por um cateto de metros e um outro dado pela diferença entre a altura do prédio e a altura do poste.
Resposta
metros.
Exercício Resolvido #6
(UFG).
Uma pista retangular para caminhada mede por metros. Deseja-se marcar um ponto , conforme figura a seguir, de modo que o comprimento do percurso seja a metade do comprimento total da pista. Calcule a distância entre os pontos e .
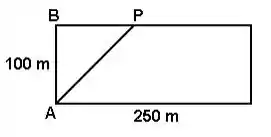
Passo 1
Sabemos que a soma dos lados do triângulo equivale à metade da soma dos lados retângulo, sendo assim, temos:
Como sabemos o valor de também podemos substituir na fórmula:
Isolando , temos:
Passo 2
O triângulo é um triângulo retângulo, portanto, podemos aplicar Pitágoras para descobrir o valor de .
Como isolamos a hipotenusa anteriormente, chegamos em uma equação em que a única incógnita será :
Resposta
metros.
Exercício Resolvido #7
Vestibular – PUC.
A soma dos quadrados dos três lados de um triângulo retângulo é igual a 32 metros. Quanto mede a hipotenusa do triângulo?
Passo 1
Inicialmente podemos não conseguir responder de maneira direta.
Temos três incógnitas, , e , sendo a hipotenusa.
Sabemos que a soma dos três lados é igual a 32, logo:
Também sabemos pelo teorema de Pitágoras que:
Dessa forma, podemos escrever a equação de Pitágoras dentro da primeira equação para obter apenas uma incógnita:
Passo 2
Agora basta resolver a equação para saber quanto mede a hipotenusa.
Resposta
metros.
Exercício Resolvido #8
Enem.
Na figura abaixo, que representa o projeto de uma escada com 5 degraus de mesma altura, o comprimento total do corrimão é igual a:
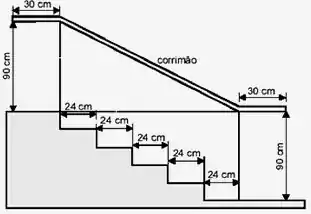
a) 1,8 m
b) 1,9 m
c) 2,0 m
d) 2,1 m
e) 2,2 m
Passo 1
O comprimento do corrimão é dado por duas partes horizontais de centímetros e uma parte inclinada.
A parte inclinada pode ser dita como a hipotenusa de um triângulo retângulo e os valores dos seus catetos é dada pela altura do corrimão e o comprimento dos degraus.
1º Cateto .
2º Cateto
Dessa forma podemos usar Pitágoras para achar o valor da hipotenusa:
Passo 2
Para saber o comprimento total devemos somar as duas partes de centímetros ao valor encontrado
Como o exercício pede a resposta em metros, precisamos converter.
Sendo assim, precisamos dividir o valor encontrado por para saber quanto ele vale em metros:
Resposta
Alternativa d).