Semelhança de Triângulos
Produzido por Marcelo LuizTeoria
Fala aí, tudo tranquilo?
Provavelmente você já ouviu falar sobre essa tal semelhança de triângulos, mas o que será que realmente significa isso?
Introdução
Definição: Há semelhança de triângulo quando essas figuras geométricas possuem ângulos congruentes e por consequência, seus lados também são correspondentes.
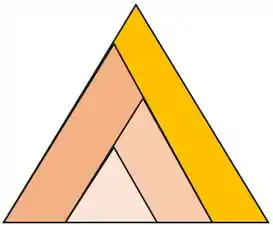
Possuir ângulos congruentes significa dizer que o valor de seus ângulos são equivalentes um a um.
Ou seja:
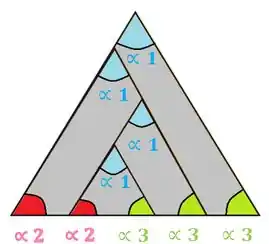
- Todos os ângulos são equivalentes;
- Todos os ângulos são equivalentes;
- Todos os ângulos são equivalentes.
Perceba que se os ângulos são equivalentes, o comprimento dos lados também será
Casos de semelhança
Os casos de semelhança entre os triângulos podem ser divididos em três tipos:
1º - AA (ângulo, ângulo) - Dois triângulos serão semelhantes se dois ângulos de um forem iguais a dois ângulos do outro.
2º - LLL (lado, lado, lado) – Dois triângulos serão semelhantes se seus três lados forem proporcionais entre si.
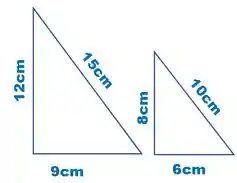
Para verificar se realmente sã semelhantes pode encontrar a razão dividindo o lado de um dos triângulos pelo seu correspondente no outro triângulo.
Caso a razão de todos os lados sejam iguais, podemos dizer que são proporcionais.
Onde será a razão de proporcionalidade.
Simplificando as frações, temos que:
Dividindo por :
Dividindo por :
Dividindo por
Dessa forma, conseguimos comprovar que os triângulos são semelhantes e a razão entre eles é .
3º - LAL (lado, ângulo, lado) – Dois triângulos serão semelhantes se possuírem um ângulo congruente entre dois lados proporcionais.
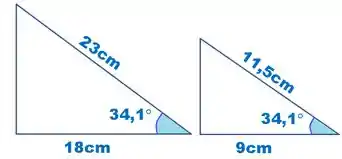
Como os ângulos são iguais, basta ver a proporção entre os lados. Caso sejam a mesma, os triângulos serão semelhantes.
Dividindo por , temos:
Dividindo por , temos:
A razão entre os lados é igual, logo pelo critério LAL os triângulos são semelhantes.
Teorema da semelhança
Quando adicionamos uma reta paralela a um dos lados do triângulo de modo que esta intercepte os dois outros lados em pontos diferentes, forma-se um novo triângulo semelhante primeiro.
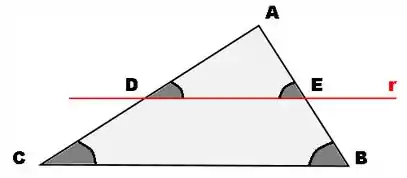
Sabendo disso, podemos fazer várias análises quando nos deparamos com imagens como essa:
1º
2º
- Os lados e são equivalentes.
- Os lados e são equivalentes.
- Os lados e são equivalentes.
3º
O triângulo é proporcional ao triângulo .
E aí, bora fazer exercícios para fixar essas idéias?
Casos de semelhança
Teorema da semelhança
Exercícios Resolvidos
Exercício Resolvido #1
Autoria própria.
Qual caso garante a semelhança entre os triângulos abaixo?
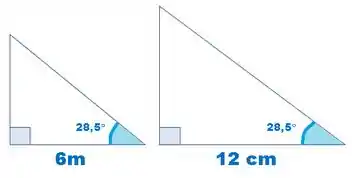
Passo 1
Existem três casos que asseguram a semelhança entre os triângulos:
1º LLL – Lado, lado e lado.
Esse caso não se aplica pois conhecemos o valor de apenas um dos lados de cada triângulo.
2º LAL – Lado, ângulo e lado.
Também não podemos tomar esse caso como base pois precisaríamos saber o valor de dois lados que estão juntos a um ângulo conhecido.
3º AA – Ângulo e ângulo.
Esse caso nos diz que se dois triângulos possuem dois ângulos iguais, eles serão semelhantes.
A imagem mostra que ambos possuem um ângulo de e como trata-se de um triângulo retângulo, os dois também possuem um ângulo de .
Logo, os triângulos são semelhantes.
Resposta
Caso AA.
Exercício Resolvido #2
Autoria própria.
Um triângulo tem seus lados dados por:
- Lado 1 ;
- Lado 2 ;
- Lado 3 .
Qual será a medida dos lados de um triângulo cuja razão é vezes maior que o primeiro triângulo?
Passo 1
A razão é dada em triângulos semelhantes pela divisão de um dos lados de um triângulo pelo lado correspondente do outro triângulo.
Como o enunciado já nos dá essa razão, basta multiplicar por cada lado do primeiro triângulo e assim, saberemos os valores dos lados do segundo triângulo.
Lado 1:
Lado 2:
Lado 3:
Resposta
Lado 1 ;
Lado 2 ;
Lado 3 .
Exercício Resolvido #3
Exercício Semelhança de triângulos – Brasil Escola – Adaptado.
Existem alguns procedimentos que podem ser usados para descobrir se dois triângulos são semelhantes sem ter de analisar a proporcionalidade de todos os lados e, ao mesmo tempo, as medidas de todos os ângulos desses triângulos. A respeito desses casos, determine quais alternativas estão incorretas e quais estão corretas:
a) Para que dois triângulos sejam semelhantes, basta que eles tenham três ângulos correspondentes congruentes.
b) Para que dois triângulos sejam semelhantes, basta que eles tenham dois lados proporcionais e um ângulo congruente, em qualquer ordem.
c) Dois triângulos que possuem apenas dois ângulos correspondentes congruentes não podem ser considerados semelhantes.
d) Para que dois triângulos sejam congruentes, basta que eles tenham os três lados correspondentes com medidas proporcionais.
Passo 1
Letra a)
Incorreta!
Para ser semelhante, basta que dois ângulos sejam congruentes pois o outro também será por consequência.
Passo 2
Letra b)
Incorreta!
Para que sejam semelhantes e se enquadrem no caso LAL (Lado, ângulo, lado), o ângulo necessariamente precisa estar entre os lados proporcionais.
Passo 3
Letra c)
Incorreta!
Se os triângulos possuírem dois ângulos iguais eles serão semelhantes, garantido pelo caso AA (Ângulo, ângulo).
Passo 4
Letra d)
Correta!
A afirmativa está correta e é garantida pelo caso LLL (Lado, lado, lado).
Resposta
a) Incorreta.
b) Incorreta.
c) Incorreta.
d) Correta.
Exercício Resolvido #4
Vestibular Unesp.
A sombra de um prédio, em um terreno plano, em uma determinada hora do dia, mede 15 m. Nesse mesmo instante, próximo ao prédio, a sombra de um poste de altura 5 m mede 3 m. A altura do prédio, em metros, é:
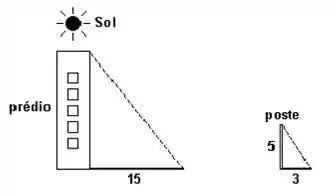
Passo 1
Observe que a área de sombra é proporcional nos dois casos pelo fato do sol ser o mesmo para ambos.
Podemos então aplicar uma regra de 3, por se tratar de triângulos semelhantes.
A altura do poste está para a sombra do poste assim como a altura do prédio está para a sombra do prédio:
Multiplicando cruzado, temos:
Resposta
metros.
Exercício Resolvido #5
Autoria própria.
Sabendo que os triângulos abaixo são semelhantes, determine:
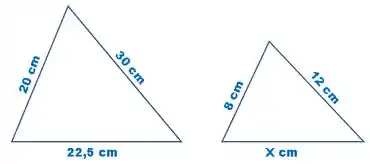
a) O valor de .
b) A razão entre os triângulos.
Passo 1
Letra a)
Como o enunciado nos diz que os triângulos são semelhantes, podemos encontrar o valor de por meio de uma regra de 3 simples.
Escolhendo o lado que contém a incógnita eu um outro qualquer, temos:
Multiplicando cruzado, temos:
Passo 2
Letra b)
Para saber a razão entre os triângulos basta escolher um lado de um e dividir pelo lado correspondente do outro:
Resposta
a) .
b) .
Exercício Resolvido #6
Autoria própria.
Estudando os triângulos determine o valor de , sabendo que os lados e são paralelos.
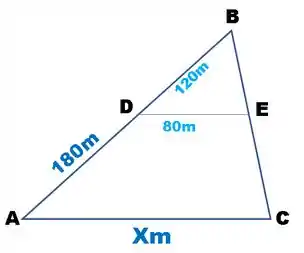
Passo 1
Repara que o triângulo e o triângulo compartilham o mesmo ângulo .
Como as retas e são paralelas, temos que o ângulo e que o ângulo ,
Ou seja, os ângulos do triangulo e são iguais. Deste modo, conseguimos aplicar a semelhança de triângulos para descobrir o valor de .
Passo 2
Na semelhança de triângulo, podemos correlacionar dois lados de cada triângulo por uma regra de 3.
O problema forneceu os lados e do triângulo
Agora vamos olhar para o triângulo . Para descobri o valor do lado , precisamos somar as partes e .
Agora é só montar a nossa regra de 3 e achar .
Passo 3
Olhando para o triângulo, temos que correlacionar os lados que são paralelos entre si. Então temos que o lado AB está para o lado . Assim como, o lado está para
Multiplicando cruzado, temos:
Resposta
metros.
Exercício Resolvido #7
Questão de concurso.
Dado dois triângulos semelhantes, sabendo que a razão de semelhança é igual a e que as medidas dos lados do triângulo maior são iguais a , e , qual é o perímetro do triângulo menor?
Passo 1
Primeiramente devemos descobrir o tamanho de cada lado do triângulo menor multiplicando o triângulo maior pela razão.
Lado 1:
Lado 2:
Lado 3:
Passo 2
Agora basta somarmos os lados para saber o valor do perímetro:
Resposta
.
Exercício Resolvido #8
Cefet/MG – 2015.
A ilustração a seguir representa uma mesa de sinuca retangular, de largura e comprimento iguais a 1,5 e 2,0 m, respectivamente. Um jogador deve lançar a bola branca do ponto e acertar a preta no ponto , sem acertar em nenhuma outra, antes. Como a amarela está no ponto A, esse jogador lançará a bola branca até o ponto , de modo que a mesma possa rebater e colidir com a preta.
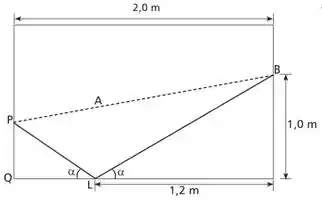
Se o ângulo da trajetória de incidência da bola na lateral da mesa e o ângulo de rebatimento são iguais, como mostra a figura, então a distância de a , em , é aproximadamente:
a) 67
b) 70
c) 74
d) 81
Passo 1
Para encontrarmos o valor da distância, precisamos encontrar dois triângulos semelhantes.
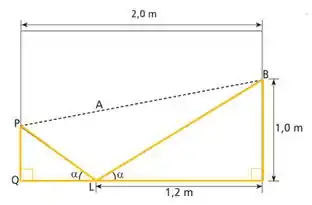
Como na figura os dois triângulos possuem um ângulo de e os dois também possuem um ângulo . Eles seguramente são semelhantes pelo caso AA (Ângulo, ângulo).
Passo 2
Precisamos agora descobrir o valor da distância entre e .
Como sabemos que o comprimento total desse lado da mesa vale metros, o valor da distância de a será:
Passo 3
Finalmente, podemos aplicar uma regra de 3 para descobrir o valor da distância de a :
Multiplicando cruzado, temos:
Resposta
Alternativa a).