Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Função Definida por Partes

Ver Todos os Exercícios

Teoria

As funções definidas por partes são aquelas definidas por 2 ou mais expressões como no exemplo abaixo:

Pode parecer um pouco confuso, mas é tranquilo, o importante é sempre ficar atento aos limites permitidos de .

Por exemplo, qual o valor de ? Primeiro a gente observa que é menor do que ! Então a função será . E agora é só aplicar:

E se, por exemplo, ? A gente vê que é maior do que , então nesse caso , aplicando vamos ter:

Para resolver funções definidas por partes é só ficar atento aos limites de

Gráfico de uma função definida por partes

Vamos ver agora uma outra função definida por partes

A forma mais fácil de esboçar o gráfico da função por partes é primeiro esboçar o gráfico de cada expressão separadamente!

Então, vamos pro exemplo. Primeiro, vamos esboçar o gráfico de .

Essa é uma função de segundo grau com coeficiente positivo, ou seja, tem concavidade pra cima. Além disso, se a gente aplicar a fórmula de Bhaskara, vamos encontrar: . Então o gráfico vai ser mais ou menos assim:

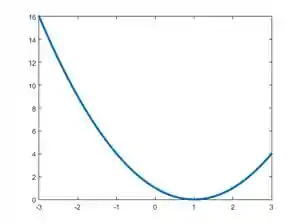
Gráfico de
Gráfico de

Em seguida, a gente esboça o gráfico da segunda expressão , uma função de primeiro grau que gera um reta, que corta o eixo em:

e o eixo em:

Então, quando a gente esboçar o gráfico vai ficar desse jeito (em vermelho)

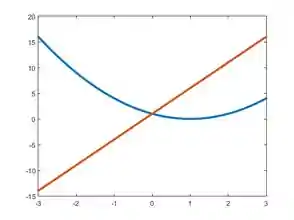
Gráfico de
Gráfico de

Com as duas curvas traçadas, podemos então limitar o gráfico de acordo com os intervalos de cada expressão.

A curva (azul) só é válida quando , então podemos apagar tudo que vem antes.

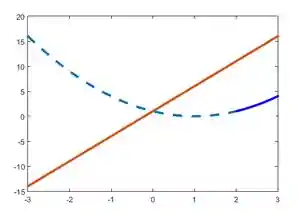
Apagando a curva azul para todos os valores de
Apagando a curva azul para todos os valores de

E o mesmo raciocínio vale para a reta. A expressão só vale pra valores de , então podemos apagar tudo que vem depois:

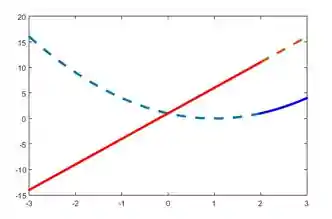
Apagando a curva vermelha para valores de
Apagando a curva vermelha para valores de

E o nosso esboço está quase pronto.

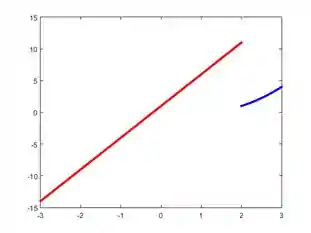
Esboço do gráfico incompleto
Esboço do gráfico incompleto

A última coisa a considerar é o ponto .

No caso desse gráfico, o ponto faz parte da expressão (azul), então devemos marcar o ponto com uma bolinha preenchida:

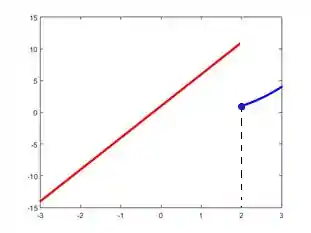
Esboço do gráfico com limite fechado na curva azul
Esboço do gráfico com limite fechado na curva azul

Por outro lado, o ponto não faz parte da expressão (vermelha), então devemos marcar o ponto com uma bolinha vazia:

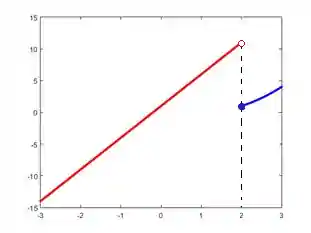
Esboço do gráfico com limite aberto na linha vermelha e limite fechado na curva azul
Esboço do gráfico com limite aberto na linha vermelha e limite fechado na curva azul

E é isso! O esboço do gráfico de uma função definida por partes está pronto!

Quer aprender mais sobre funções definidas por partes? Então da uma olhada nessa aula completona!

Gráfico de uma função definida por partes

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Determine a expressão matemática da função f x , para que ela valha x 4 apenas no intervalo [ - 2,2 ] .

Nos demais pontos, a função deve valer 0 .

Passo 1

Para tal precisamos restringir o intervalo de validade da função. Assim, escrevemos:

f x = x 4 , - 2 ≤ x ≤ 2 0 , r e s t o

Passo 2

Onde “resto” denota tudo aquilo que está fora do intervalo [ - 2,2 ] , ou seja, seria assim

f x = x 4 , - 2 ≤ x ≤ 2 0 , - 2 > x       o u       x > 2

Resposta

f x = x 4 , - 2 ≤ x ≤ 2 0 , - 2 > x       o u       x > 2

Exercício Resolvido #2

Elaboração Própria

Determine os valores máximos e mínimos da seguinte função:

f x = sen ⁡ x ,     x < π x 2 - π x ,     x ≥ π

Passo 1

Temos que a função tem expressão sen ⁡ x para todo x < π . Enquanto x 2 - π x tem raízes:

x 1 = 0 x 2 = π

E vértice:

x v = - b 2 a = π 2

E:

y v = - Δ 4 a = - π 2 4

Formando o gráfico:

Passo 2

Observando a função, vemos que não tem ponto de máximo, pois a parte da parábola cresce indefinidamente e o mínimo é ditado pelos mínimos do seno que começam x = - π / 2 e se repetem a cada 2 π indo para a esquerda.

Resposta

Pontos de máximo: não há

Pontos de mínimo: - π 2 - 2 π ⋅ k ,   k = 0,1 , 2,3 …