A Forma Complexa da Série de Fourier
Produzido por Carolina SabaTeoria
Essa série de Fourier irritante ainda tem um tópico que lhe aguarda, jovem gafanhoto. Existem questões que pedem a forma complexa da série!
Whaaaat??? Forma complexa?!?! Isso! Aquela com a unidade imaginária . Não se assuste, a forma complexa deixa a expressão bem mais curtinha. Sem mais enrolação, te apresento a forma complexa da série de Fourier:
Onde e é o coeficiente da série complexa.
Vamos agora entender como chegamos a essa forma que chamamos complexa:
Forma de Euler
Primeiro vamos relembrar duas relações importantes, chamadas relações de Euler:
Agora vamos substituir na equação da série de Fourier:
Arrumando:
Vamos dar uma pausa e vamos ver uma relação com o sinal dos coeficientes:
Cálculo de :
Então:
Cálculo de :
Então:
Agora vamos chamar:
Assim, nossa expressão pode ser escrita como:
Trocando por no segundo somatório:
Note que:
Então:
Agora se liga numa coisa: o primeiro somatório vai de 1 até e o segundo de até -1. Po, cadê o termo ? Isso mesmo, é o termo , pois se ambas as exponenciais vão ser 0 e só teremos . Portanto, a gente pode juntar todo mundo num somatório só!
Pois é, com esse algebrismo todo chegamos a chamada Forma complexa da série de Fourier .
Existe uma forma mais simples de chegarmos ao sem precisar calcular e , ele é calculado por:
É importante observar que essa forma, apesar do nome de complexa, ela é real, pois é igual a forma original de Fourier.
Como obter a forma de -L a L?
Vamos supor que queremos a forma complexa da função , e . Bem o primeiro ponto é descobrir o valor de . Como a função tem período 2, temos:
Agora, vamos ao cálculo do , usando a fórmula lá de cima
Certo? ERRADO!!! A nossa função só está definida com aquela expressão de 0 a 2. Na integral, estamos dizendo que ela vale , também de -1 a 0 o que não é verdade.
Para te provar isso, deixa eu fazer um desenhinho do gráfico dessa função
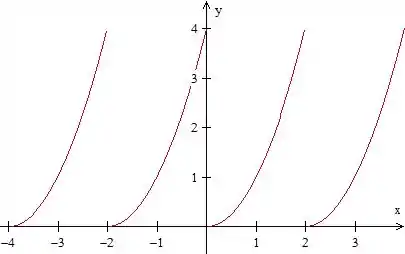
São vários braços de parábola, porque a função é periódica (não se esqueça disso!). Se você pegar teríamos . No gráfico, a gente percebe que, na verdade, o valor da função é maior do que . Isso porque a expressão só vale de 0 a 2.
Então o que devemos fazer? Você concorda que esses braços nada mais são do que deslocamentos da função dada no enunciado? E como deslocamos um gráfico? Se você quer deslocar o gráfico de unidades para a esquerda, devemos fazer . Se você quiser deslocar para a direita, você faz .
Aqui, a gente sabe que de 0 a 2, Queremos obter a expressão, deslocando esse gráfico para a esquerda, sabemos que o deslocamento corresponde ao valor do período. Então a expressão de -2 a 0 será:
Então podemos escrever o seguinte:
Agora sim podemos calcular os coeficientes da seguinte forma:
Dividimos o intervalo de integração em cada parte aonde temos a expressão da função! Depois é só fazer tudinho como estamos acostumados! Partiu exercícios!
Como obter a forma f ( x ) de -L a L?
Exercícios Resolvidos
Exercício Resolvido #1
Cálculo Avançado A – CEFET-RJ - Lista de exercício de série de Fourier - 20
Encontre a série complexa de Fourier de , se e
Passo 1
Primeiro, repara que o período da função é , então:
Para fazermos a série complexa precisamos achar a forma de entre e .
Assim, encontramos a função entre e .
Passo 2
Precisamos agora encontrar a Série complexa de Fourier de , a fórmula é:
E a fórmula do coeficiente é:
Assim, precisamos calcular os coeficientes para encontrarmos a série, então:
Assim, separando nos intervalos, temos:
Calma, chegando nessa expressão, temos que realizar operações para reduzi-la.
Assim, vamos lembrar que:
Então
Com isso, podemos cancelar as duas parcelas com o . Assim, chegamos a:
Mas lembrando que:
Temos:
Assim, chegamos a forma mais simplificada da série:
Resposta
Exercício Resolvido #2
Ache a série de Fourier complexa para a função , se e
Passo 1
Primeiro, é fácil ver que o período da função é , então:
Para fazermos a série complexa precisamos achar a forma de entre e .
Assim, encontramos a função entre e .
Ah! E veja que:
Isso facilitará e muito nossas contas!
Passo 2
Precisamos agora encontrar a Série complexa de Fourier de , a fórmula é:
E a fórmula do coeficiente é:
Como a função é par, é mais fácil trabalharmos com , e e depois relacionar com:
Passo 3
Dessa forma, como é par podemos escrever:
Calculando temos:
Lembrando que
Passo 4
Agora vamos calcular os ’s. Temos que:
Assim, podemos escrever:
Lembrando que:
E integrando, podemos escrever:
Mas atenção! Note que isso não vale para e ! E que para
Passo 5
Vamos então calcular e :
E
Com isso, temos os valores de :
Resposta
Exercício Resolvido #3
Ache, por integração direta, a série de Fourier complexa para a função , se e .
Passo 1
Primeiro, é fácil ver que o período da função é , então:
Para fazermos a série complexa precisamos achar a forma de entre e .
Assim, encontramos a função entre e .
Passo 2
Precisamos agora encontrar a Série complexa de Fourier de , a fórmula é:
E a fórmula do coeficiente é:
Assim, precisamos calcular os coeficientes para encontrarmos a série, então:
Assim, separando nos intervalos, temos:
Calma, chegando nessa expressão, temos que realizar operações para reduzi-la.
Assim, vamos lembrar que:
Então
Com isso, podemos cancelar as duas parcelas com o . Assim, chegamos a:
Assim, chegamos a forma mais simplificada da série: