Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Fatores que influenciam na difusão

Ver Todos os Exercícios

Teoria

E aí, tudo bem?

Notem na imagem abaixo e imaginem que o cobre seria um carro fazendo um role da esquerda para a direita e o Niquel da direita para a esquerda, essa mão de duas vias é a difusão dos átomos, sabe os buracos nas estaradas? Influenciam na velocidade dos carros certo? Vamos ver o que influencia na movimentação dos átomos ?

Espécies difusivas

A intensidade do coeficiente de difusão (D) é uma indicação da taxa que os átomos se difundem.. As espécies difusivas, bem como o material base, influenciam o coeficiente de difusão. Por exemplo, existe uma diferença gigantesca na magnitude entre a autodifusão e a interdifusão do carbono no ferro α a 500ºC, e o valor de D é maior para a interdifusão do carbono (3,0x10 -21 contra 2,4x10 -12 m 2 /s). Essa comparação também pode ser vistas na difusão por lacuna e intersticial. Viram como se diferenciam ?? Vejam outras variações na tabela ali em baixo.

Temperatura

A temperatura é uma outra variável que influência muuuuuuito nas taxas de difusão. Por exemplo, olhando a tabela acima, para a autodifusão do Fe no Fe α, o coeficiente de difusão aumenta (de 3,0x10 -21 para 1,8x10 -15 m2/s) ao se elevar a temperatura de 500 para 900ºC e essa dependência é expressa por:

D = D 0 exp ⁡ - Q R T

Onde:

D0: constante pré-exponencial (m2/s), para energia de ativação para a difusão (J/mol, cal/mol)

R é a constante dos gases (8,31 J/mol-K, 1,987 cal/mol-K ou 8,62x10-5) eV/átomo

T : temperatura absoluta (K)

E o que é enrgia de ativação??

Essa energia de ativação pode ser avaliada como a energia indispensável para causar o movimento difusivo de um mol de átomos. Uma energia de ativação alta deriva em um coeficiente de difusão relativamente baixo.

E aii vamos aplicar os conhecimentos que aprendemos agora?

A constante pré-exponencial e a energia de ativação do Fe em cobalto são dados. Em qual temperatura o coeficiente de difusão terá o valor de 1,5x10 --13 m 2 ⁄s.

Dados:

Do: 1,05 x10 --4 m 2 ⁄s.

Qd: 125600 J/mol

D: 1,5x10 --13 m 2/s

T?

D = D 0 exp ⁡ - Q R T

  1,5 x 10 - 13 = 1 , 05 x 10 - 4 exp ⁡ - 125600   8,31 T

Para resolvermos esta exponencial basta aplicarmos sua função inversa em ambos os lados da equação.

ln ⁡ 1,5 x 10 - 13 = ln ⁡ 1,05 x 10 - 4 - 125600   8,31 T ⁡

- 29,53 = - 9,16 - 15114,32 t ⁡

- 29,53 t = - 9,16 - 15114,32 ⁡

t = 512   k

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Sobre o processo de difusão determine:

  1. A difusão é um processo termicamente ativado e a taxa de difusão depende exclusivamente do par soluto-solvente
  2. A difusão é um processo termicamente ativado e a taxa de difusão não depende das estruturas cristalinas.
  3. A difusão é um processo termicamente ativado e a taxa de difusão depende do par soluto-solvente e de suas estruturas cristalinas.

Passo 1

A difusão é um processo termicamente ativado e a taxa de difusão depende do par soluto-solvente e de suas estruturas cristalinas.

Resposta

Alternativa C

Exercício Resolvido #2

Elaboração própria

Determine qual é a influência da temperatura na difusão atômica:

  1. Conforme a temperatura aumenta, ocorre uma redução das lacunas e consequentemente uma menor difusão.
  2. Conforme a temperatura aumenta a energia térmica reduz
  3. O aumento da temperatura favorece em uma maior difusão.

Passo 1

Conforme a temperatura aumenta, ocorre um aumento das lacunas e consequentemente uma maior difusão.

Passo 2

Ocorrendo um aumento da energia térmica, aumentando a difusão.

Resposta

Alternativa C

Exercício Resolvido #3

Elaboração própria

Sobre a energia de ativação determine a resposta correta:

  1. A energia para difusão intersticial é menor que para difusão em lacuna.
  2. A energia de ativação não é influenciada pelo tipo de átomo e estrutura.
  3. Quanto menor e a energia maior é a velocidade do processo e maior a sensibilidade com a temperatura.

Passo 1

A energia para difusão intersticial é menor que para difusão em lacuna.

Passo 2

A energia de ativação é influenciada pelo tipo de átomo e estrutura.

Passo 3

Quanto maior e a energia menor é a velocidade do processo e maior a sensibilidade com a temperatura.

Resposta

Alternativa A

Exercício Resolvido #4

Elaboração própria

Sobre a influência da microestrutura na difusão atômica.

  1. A difusão ocorre mais rápido em materiais monocristalinos.
  2. Ocorre com maior facilidade em estruturas com menos restrições
  3. Os caminhos de difusão dos materiais não influenciam no coeficiente de difusão.

Passo 1

A difusão ocorre mais rápido em materiais policristalinos.

Passo 2

Ocorre com maior facilidade em estruturas com menos restrições

Passo 3

Os caminhos de difusão dos materiais influenciam no coeficiente de difusão.

Resposta

Alternativa B

Exercício Resolvido #5

Elaboração própria

Das características a seguir determine os fatores que influenciam negativamente na difusão:

  1. Baixo empacotamento, baixo ponto de fusão e elevada densidade
  2. Ligações fortes, boa qualidade cristalina, baixo ponto de fusão
  3. Elevado empacotamento, ponto de fusão e grande raio atômico.

Passo 1

Elevado empacotamento, ponto de fusão e densidade

Passo 2

Ligações fortes, boa qualidade cristalina, elevado ponto de fusão

Passo 3

Elevado empacotamento, ponto de fusão e grande raio atômico.

Resposta

Alternativa C

Exercício Resolvido #6

Elaboração própria

Analise as curvas experimentais do coeficiente de auto-difusão na prata. E avalie a influência da temperatura.

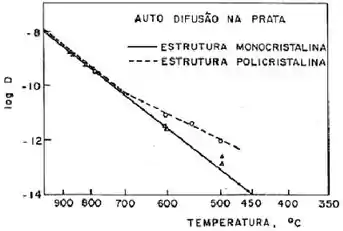
Passo 1

Em temperaturas altas, o coeficiente de difusão é elevado no cristal, promovendo o movimento de átomos na rede, sendo desprezível, portanto, a difusão em contornos de grão.

Passo 2

Se a temperatura é decai, a difusão na rede cristalina é complicada e o reforço de contornos de grão se torna expressiva

Resposta

Em temperaturas altas, o coeficiente de difusão é elevado no cristal, promovendo o movimento de átomos na rede, sendo desprezível, portanto, a difusão em contornos de grão. Se a temperatura é decai, a difusão na rede cristalina é complicada e o reforço de contornos de grão se torna expressiva

Exercício Resolvido #7

Elaboração própria

Determine a temperatura do coeficiente de difusão para a difusão do alumínio no zinco e apresenta um valor de 2,17 x 10-10 m2/s. Considerando os dados a seguir:

Do: 1,31 x10 --3 m 2 ⁄s.

Qd: 213200 J/mol

R: 8,31 J/mol-K

Passo 1

Primeiramente devemos lembrar da equação:

D = D 0 exp ⁡ - Q R T

Passo 2

Calculando temos:

2,17   x   10 - 10 = 1,31   x 10 - 3   exp ⁡ - 213200 8,31 T

2,17   x   10 - 10 1,31   x 10 - 3 =   exp ⁡ - 213200 8,31 T

1,656 x 10 - 7   =   exp ⁡ - 213200 8,31 T (Para “retirarmos” a exponencial, aplicamos sua inversa Ln dos dois lados da equação.

ln ⁡ 1,656 x 10 - 7   =   ln  ( exp ⁡ - 213200 8,31 T )

- 15,613   =   - 213200 8,31 T ⁡

- 15,613 × 8,31 T     =   - 213200

- 129,744 T     =   - 213200

T     =   1643,23   K

Resposta

T     =   1643,23   K

Exercício Resolvido #8

Elaboração própria

Determine a temperatura do coeficiente de difusão para a difusão do ferro no aço e apresenta um valor de 1,72 x 10-13 m2/s. Considerando os dados a seguir:

Do: 2,21 x10 --5 m 2 ⁄s.

Qd: 148200 J/mol

R: 8,31 J/mol-K

Passo 1

Primeiramente devemos lembrar da equação:

D = D 0 exp ⁡ - Q R T

Passo 2

Calculando temos:

1,72   x   10 - 1 3 = 2 , 2 1   x 10 - 5   exp ⁡ - 148200 8,31 T

1,72   x   10 - 13 2,21   x 10 - 5 =   exp ⁡ - 148200 8,31 T

7,782 x 10 - 9   =   exp ⁡ - 148200 8,31 T (Para “retirarmos” a exponencial, aplicamos sua inversa Ln dos dois lados da equação.

ln ⁡ 7,782 x 10 - 9   =   ln  ( exp ⁡ - 148200 8,31 T )

- 1 8,671   =   - 148200 8,31 T ⁡

- 18,671   × 8,31 T     =   - 148200

- 155,158 T     =   - 148200

T     =   955,15   K

Resposta

T     =   1643,23   K

Exercício Resolvido #9

Capítulo 5 , Perguntas e Problemas, exercício 1 8

Em qual temperatura o coeficiente de difusão para a difusão do cobre no níquel terá um valor de 6,5 × 1 0 - 17   m 2 / s . Use os dados de difusão na Tabela 5.2 .

Passo 1

Olá! Tudo bem? Nesse problema devemos calcular a temperatura na qual o coeficiente de difusão para a difusão do cobre no níquel terá um valor de 6,5 × 1 0 - 17   m 2 / s . Utilizaremos a Tabela 5.2 (pág. 113 ; 8 ª Ed.) e a equação 5 . 9 a (pág. 11 3 ; 8 ª Ed.) para resolvermos esse exercício.

Isolando T na equação 5.9 a e inserindo os valores fornecidos pela Tabela 5.2 , temos:

T = - Q d R ln ⁡ D - ln ⁡ D 0 = 256000   J / m o l ( 8,31   J / m o l - K ) [ ln ⁡ ( 6,5 × 10 - 17   m 2 / s ) - ln ⁡ ( 2,7 × 10 - 5   m 2 / s ) ]

T = 1152   K = 879 ° C

Resposta

T = 879 ° C

Exercício Resolvido #10

Capítulo 5 , Perguntas e Problemas, exercício 1 9

A constante pré-exponencial e a energia de ativação para a difusão do ferro no cobalto são de 1,1 × 10 - 5   m 2 / s e 253 . 300   J / m o l , respectivamente. Em qual temperatura o coeficiente de difusão possuirá um valor de 2,1 × 10 - 14   m 2 / s ?

Passo 1

Olá! Tudo bem? Nesse problema devemos calcular a temperatura na qual o coeficiente de difusão para a difusão do ferro no cobalto terá um valor de 2,1 × 10 - 14   m 2 / s . Utilizaremos a Tabela 5.2 (pág. 113 ; 8 ª Ed.) e a equação 5 . 9 a (pág. 11 3 ; 8 ª Ed.) para resolvermos esse exercício.

Isolando T na equação 5.9 a e inserindo os valores fornecidos pela Tabela 5.2 , temos:

T = Q d R ln ⁡ D - ln ⁡ D 0 = 25 33 00   J / m o l ( 8,31   J / m o l - K ) [ ln ⁡ ( 1,1 × 10 - 5   m 2 / s ) - ln ⁡ ( 2,1 × 10 - 14   m 2 / s ) ]

T = 15 18   K = 1245 ° C

Resposta

T = 1245 ° C

Exercício Resolvido #11

CALLISTER, Ciências dos materiais, 8° edição, cap.5, Nº 22

Os coeficientes de difusão para prata no cobre são dados para duas temperaturas:

  1. Determine os valores de Do e Qd.
  2. Qual é a magnitude de D a 875°C.

Passo 1

  1. Para determinarmos Qd usamos simultaneamente em uma combinação de igualdade as duas equações abaixo:

    2. l n D 1 = l n D o - Q R 1 T 1

    l n D 2 = l n D o - Q R 1 T 2

    Agora nós devemos isolar Qd em relação as temperaturas T1= 923 K e T2= 1173 k e D1= e D2= 1,3 x 10 -13

    Q d = - R × l n D 1 - l n D 2 1 T 1 - 1 T 2

    Igualando as equações, podemos agora substituir os valores:

    Q d = - 8,31 × l n ⁡ ( 5,5   × 10 - 16 ) - l n l n   ( 1,3   × 10 - 13 )   1 923 - 1 1173

    Q d = 196,68 x 10³ J/mol

    Agora podemos achar “Do”:

    D o = D 1 e x p e x p   Q R T 1  

    D o = 5,5   × 10 - 16 e x p e x p   196,68   x   10 ³   8,31   × 923  

    D o = 7,53 × 10 - 5 m 2 / s  

    Passo 2

    Agora devemos calcular para a temperatura de 1148 K

    l n D 1 = l n D o - Q R 1 T 1

    D = 7,53 × 10 - 5 e x p   - 196,68   x   10 ³   8,31   × 1148  

    D = 8,3 × 10 - 14 m 2 / s

    Resposta

    a )   D o = 7,53 × 10 - 5 m 2 / s   e Q d = 196,68 x 10³ J/mol

  2. D = 8,3 × 10 - 14 m 2 / s

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

A energia de ativação para a difusão do carbono no cromo é de 111.000J / m o l . Calcule o coeficiente de difusão a 1100K( 827 ° C ) , dado que o valor de D a 1400K( 1127 ° C ) é de 6,25 × 10 - 11m 2
A figura a seguir mostra um gráfico do logaritmo (para a base 10) do coeficiente de difusão em função do inverso da temperatura absoluta, para a difusão do ferro no cromo. Determine os valores para a
Em qual temperatura o coeficiente de difusão para a difusão do cobre no níquel terá um valor de 6,5 × 1 0 - 17m 2 / s . Use os dados de difusão na Tabela 5.2 .
Usando os dados na Tabela 5.2 , calcule o valor de D para a difusão de zinco no cobre a 650 ° C .
A constante pré-exponencial e a energia de ativação para a difusão do ferro no cobalto são de 1,1 × 10 - 5m 2 / s e 253 . 300J / m o l , respectivamente. Em qual temperatura o coeficiente de difusão p