Índices de Miller
Teoria
Os índices de Miller são três números inteiros
-Quee?! 😖
Vem comigo que vai ficar mais claro!
📢 Clique para saber mais:
Índices de Miller de um Plano Cristalográfico
Em uma estrutura cristalina é necessário fazer alusão a alguns planos de átomos, ou pode haver interesse em conhecer a orientação cristalográfica de um plano ou conjunto de planos de uma rede cristalina.
Para identificar planos cristalográficos, numa estrutura cristalina cúbica, usa-se o sistema de notação de Miller! Por exemplo, para uma célula cúbica de parâmetro de rede
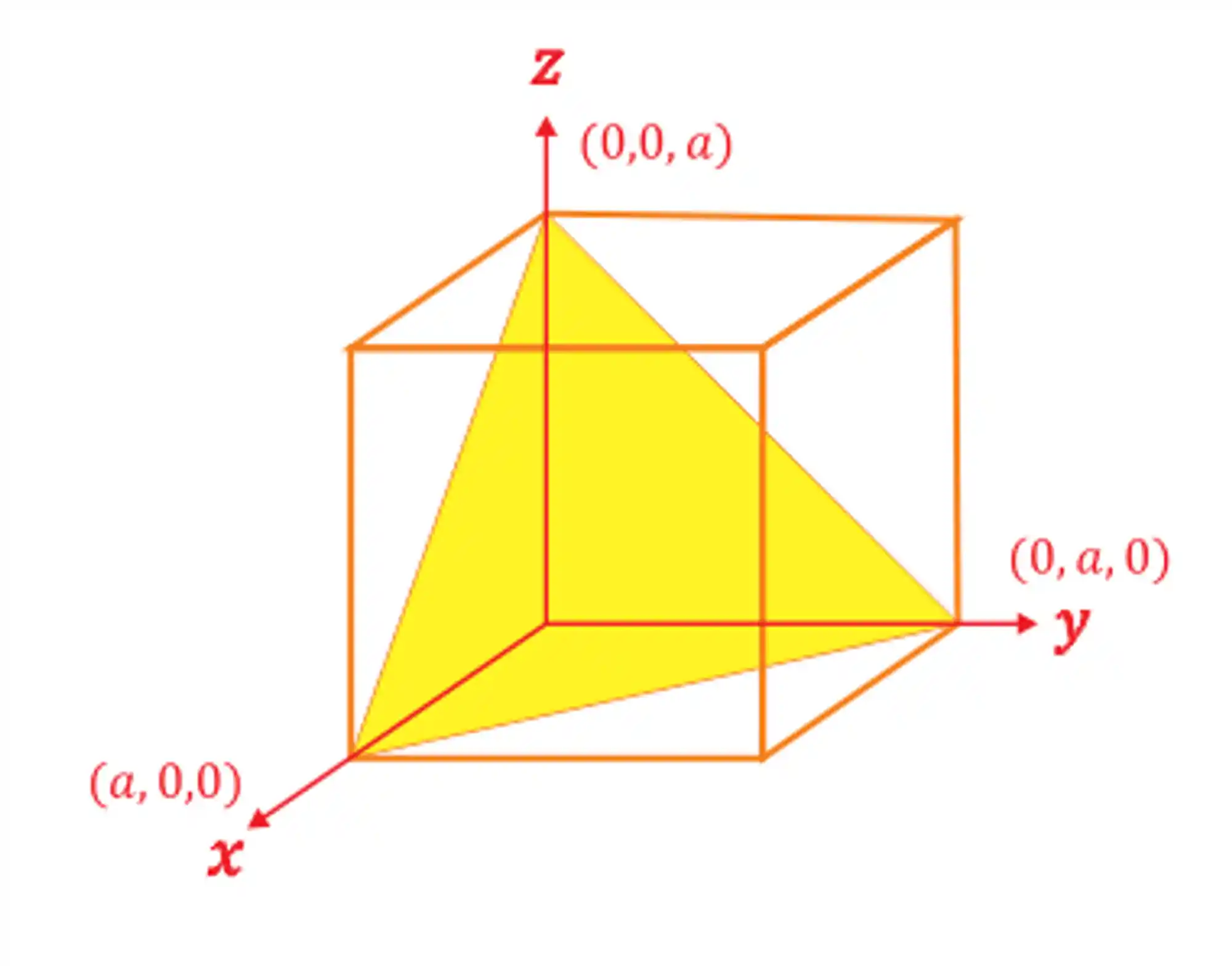
Note, que os pontos de intersecção
Índices de Miller para um Plano Paralelo a um dos Eixos
E se o plano for paralelo a um dos eixos, o que acontecerá?!
Ele nunca poderá interceptar um dos eixos, porque tende ao infinito e corresponde ao índice de Miller zero (0). Por exemplo, imagine um plano que intersecte os eixos
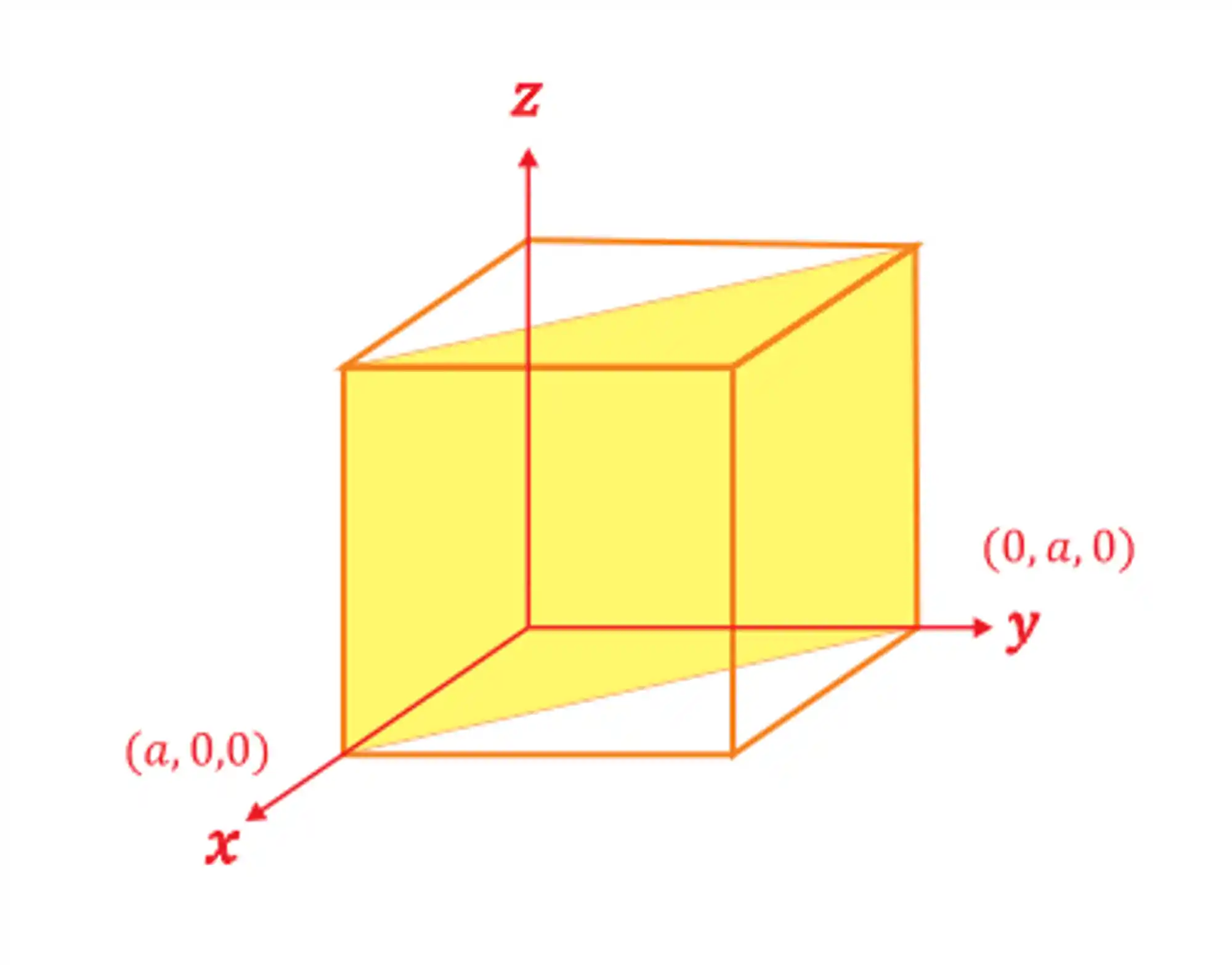
O plano intercepta
Índice de Miller: Plano de Intersecção com Eixos Fracionários
Se um plano intersectar os eixos numa fracção do parâmetro de rede, o adequado índice de Miller terá que ser seu inverso. Por exemplo, para um plano que intercepte o eixo
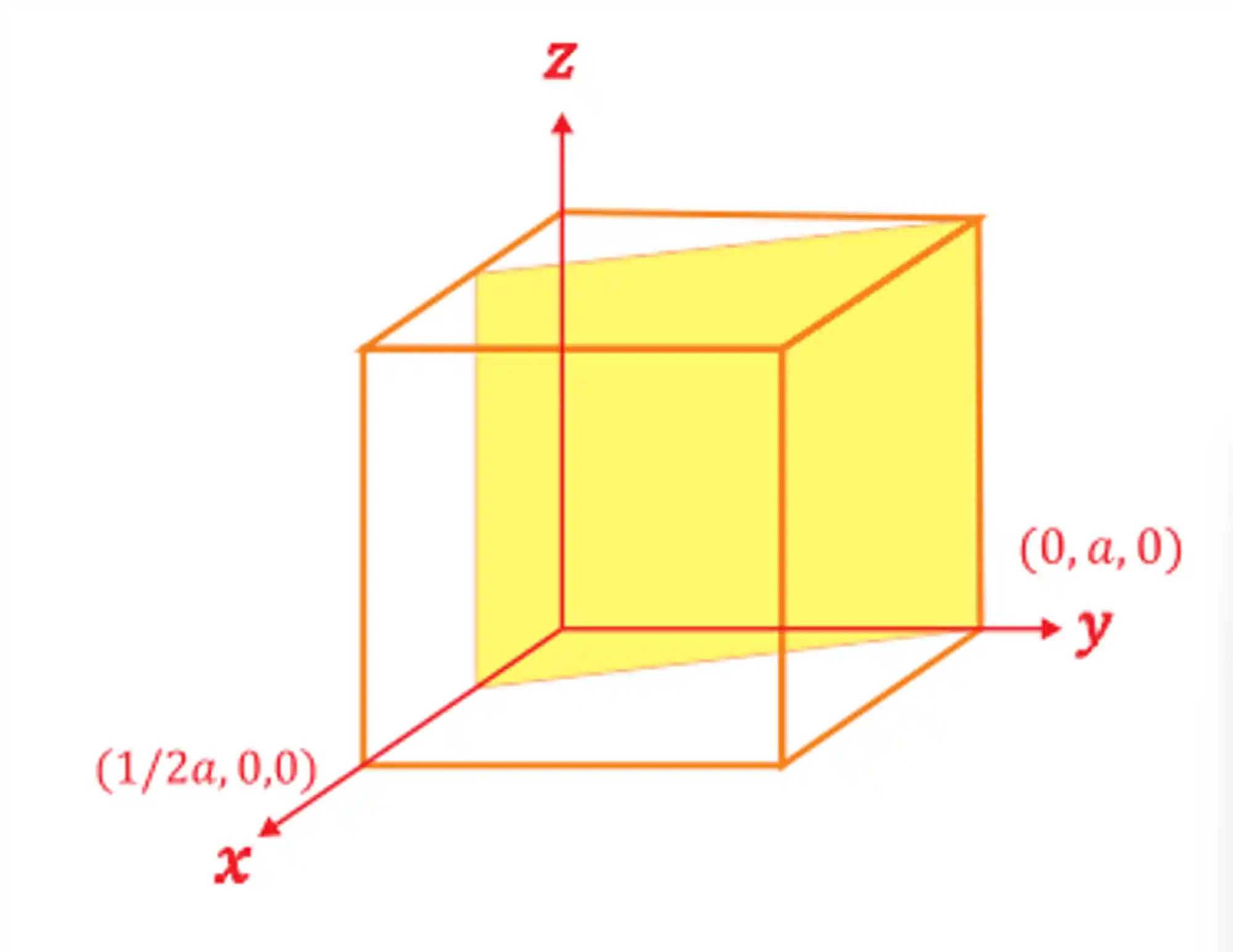
Então a intersecção é
E o que acontece se o inverso não for um número inteiro ? Vamos analisar o exemplo a seguir!
Exemplo: Quais são os valores que interceptam
- Primeiramente devemos inverter as frações:
, , - Agora devemos reduzir a inteiros, podemos multiplicar por
, vamos ver o que ocorre?
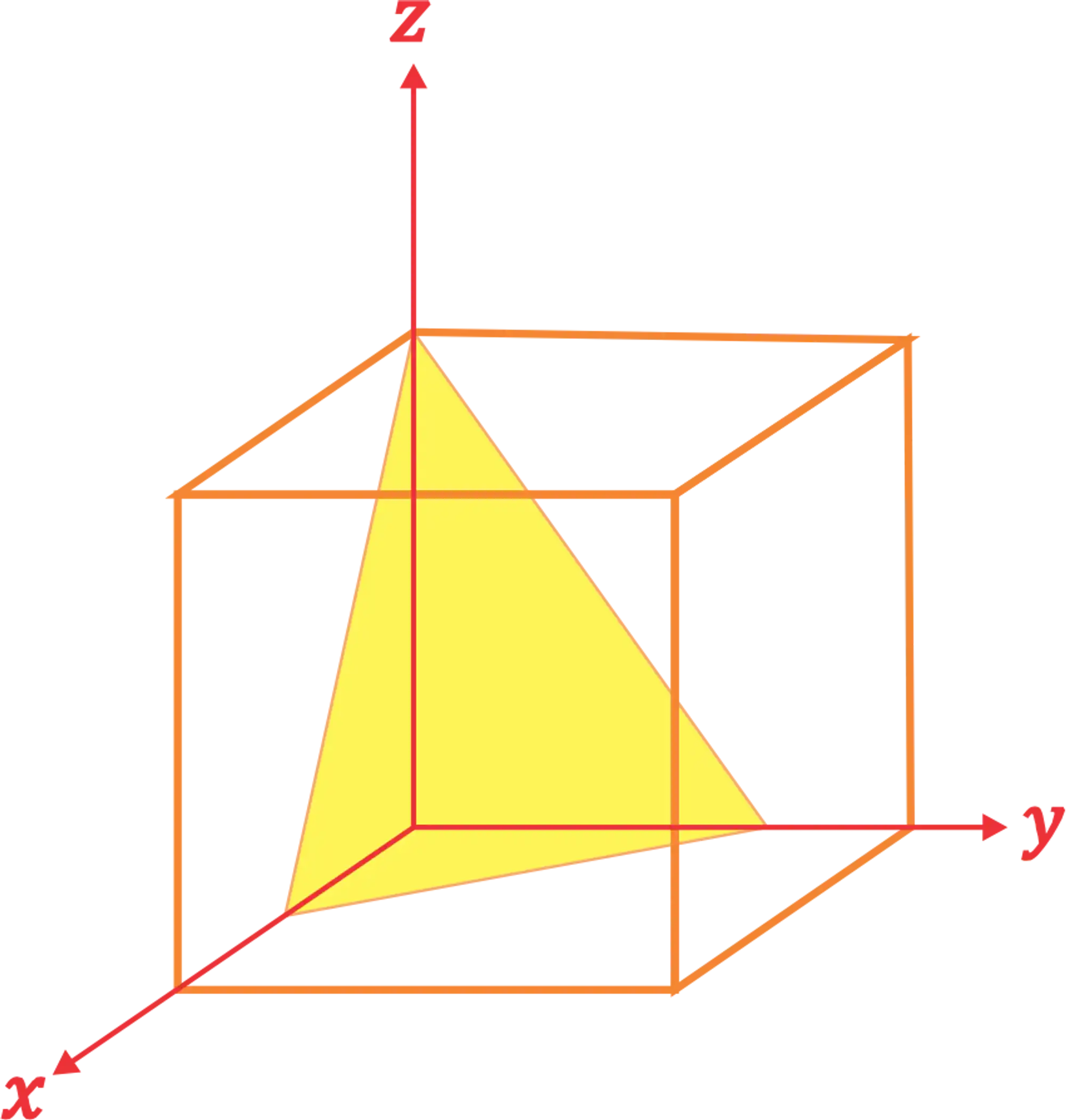
- Multiplicarmos por 3 para reduzir a fração que restou:
Índice de Miller para um Plano que Intercepta os Eixos no Lado Negativo
Para um plano paralelo a
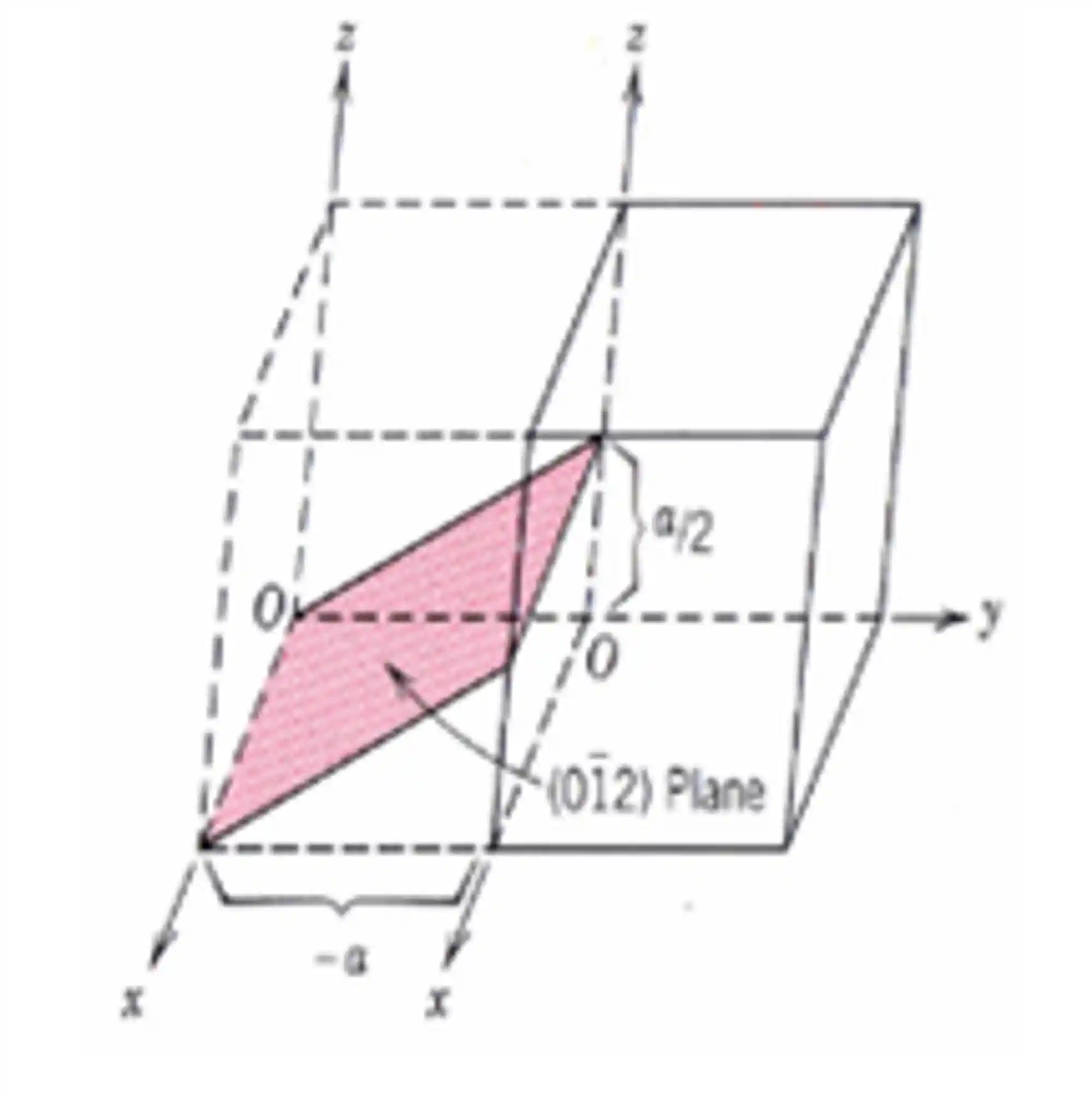
Regras para determinar os Índices de Miller de um plano
Para determinar os índices de Miller de um plano, temos que achar as posições dos pontos em que o plano intercepta os eixos
- Determinamos o inverso;
- Reduzimos tudo ao mesmo denominador, quando necessário.
- Colocamos os valores entre parênteses, pondo barras sobre os índices negativos.
Para sistemas não cúbicos os índices são determinados do mesmo modo, independentemente dos ângulos dos eixos e dos parâmetros de rede
Agora vamos praticar com exercícios?
Índices de Miller de um Plano Cristalográfico
Índices de Miller para um Plano Paralelo a um dos Eixos
Índice de Miller: Plano de Intersecção com Eixos Fracionários
Índice de Miller para um Plano que Intercepta os Eixos no Lado Negativo
Regras para determinar os Índices de Miller de um plano
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Considere as afirmativas a seguir e escolha a opção correta:
I. Num sistema cúbico, um plano e uma direção que tenham índices de Miller do mesmo valor são paralelos.
II. Quando o índice de Miller de um plano é igual a zero, esse plano é paralelo ao eixo cristalográfico correspondente a esse índice.
Passo 1
Num sistema cúbico, um plano e uma direção que tenham índices de Miller de mesmo valor são perpendiculares.
Passo 2
Quando o índice de Miller de um plano é igual a zero, esse plano é paralelo ao eixo cristalográfico correspondente a esse índice
Resposta
Alternativa II
Exercício Resolvido #2
Elaboração própria
Determine o índice de Miller do plano a seguir:
Passo 1
Primeiramente devemos observar onde o plano cruza.
Passo 2
Quando o índice de Miller de um plano é igual a zero, esse plano é paralelo ao eixo cristalográfico correspondente a esse índice, neste caso o Z.
Notem que em x e y ele intercepta o ponto 1
Resposta
(1 1 0)
Exercício Resolvido #3
Elaboração própria
Determine o índice de Miller do plano a seguir:
Passo 1
Primeiramente devemos observar onde o plano cruza. Em x e y ele “corta” no ponto 1
Passo 2
Observem que no eixo z a ponta do triangulo está em paralelo ao eixo z indicando estar no eixo negativo para z.
Resposta
)
Exercício Resolvido #4
Elaboração própria
Represente nas células unitárias abaixo o plano cristalográficos indicado: 1)
Passo 1
Temos como indicado o plano 1)notem que o plano “cortará” o eixo y em -2 e para x e z igual a 1
Passo 2
Traça uma linha de ligação em x =1 e uma com z=1 e puxe até o final da célula unitária a esquerda onde será respectivo ao eixo negativo da célula, como estará na segunda célula no eixo negativo, então encontraremos o ponto -2.
Resposta
Exercício Resolvido #5
Elaboração própria
Represente nas células unitárias abaixo o plano cristalográficos indicado:
Passo 1
Temos como indicado o plano notem que o plano “cortará” o eixo y em 1 e para z igual a -1 e x igual a 0
Passo 2
Traça uma linha de ligação em y=1 e uma com z=-1 paralelamente a z, pois este é negativo, note que terá um retângulo inclinado sem encostar no eixo x, pois este é igual a zero.
Resposta
Exercício Resolvido #6
Elaboração própria
Identifique os sistemas não cúbicos representados abaixo: 
- Monoclínico, Triclínico e Ortorrômbico
- Triclínico, Monoclínico e ortorrômbico
- Monoclínico, Ortorrômbico e Triclínico
Passo 1
Monoclínico é um sistema cristalino que se apresenta três eixos cristalográficos de comprimentos diferentes
Passo 2
O sistema cristalino ortorrômbico apresenta três eixos cristalográficos mutuamente perpendiculares, mas cada um com um comprimento
Passo 3
Triclínico exibe apenas simetria translacional ou inversão. Possui três eixos cristalográficos, todos diferentes entre si
Resposta
Alternativa C
Exercício Resolvido #7
Elaboração própria
Sobre as regras para a determinação do índice de uma direção, determine a opção correta:
- As direções não passam na origem
- Comprimento do vetor em termos de a, b, c.
- Coloca-se entre colchetes, colocando barras sobre os índices positivos.
Passo 1
As direções passam na origem
Passo 2
Comprimento do vetor em termos de a, b, c.
Passo 3
Coloca-se entre parêntesis, colocando barras sobre os índices negativos.
Resposta
Alternativa B
Exercício Resolvido #8
Elaboração própria
Represente nas células unitárias abaixo o plano cristalográficos indicado: (1 0 1 )
Passo 1
Temos como indicado o plano (1 0 1) notem que o plano não “cortará” o eixo y pois o valor é igual a zero. E para x e z igual a 1
Passo 2
Traça uma linha de ligação em x =1 e uma com z=1 e puxe até o final da célula unitária, você irá observar que o plano ficara inclinado, pois não encostara em y.
Resposta
Exercício Resolvido #9
Elaboração própria
Represente nas células unitárias abaixo o plano cristalográficos indicado: 1)
Passo 1
Temos como indicado o plano 1)notem que o plano “cortará” o eixo y em -2 e para x e z igual a 1
Passo 2
Traça uma linha de ligação em x =1 e uma com z=1 e puxe até o final da célula unitária a esquerda onde será respectivo ao eixo negativo da célula, como estará na segunda célula no eixo negativo, então encontraremos o ponto -2.
Resposta
Exercício Resolvido #10
Elaboração própria
Represente nas células unitárias abaixo o plano cristalográficos indicado:
Passo 1
Temos como indicado o plano notem que o plano “cortará” o eixo y em 1 e para z igual a -1 e x igual a 0
Passo 2
Traça uma linha de ligação em y=1 e uma com z=-1 paralelamente a z, pois este é negativo, note que terá um retângulo inclinado sem encostar no eixo x, pois este é igual a zero.
Resposta
