Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 9.Perguntas e Problemas - Ex. 15

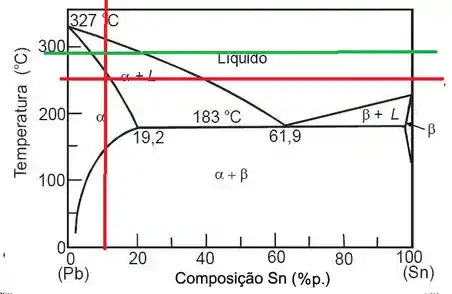
Uma amostra de 1,5 kg de uma liga com 90% Pb-10% Sn é aquecida a 250 ° C (480 ° F); nessa temperatura, ela consiste totalmente em uma solução sólida da fase α (Figura 9.8). A liga deve ser fundida até 50% da amostra fique líquida, permanecendo o restante a fase α. Isso pode ser feito pelo aquecimento da liga ou pela alteração da sua composição, mantendo-se a temperatura constante.

  1. Até que temperatura a amostra deve ser aquecida?
  2. Quanta estanho deve ser adicionada à amostra de 1,5 kg a 250 ° C para atingir esse estado?

Passo 1

  1. No diagrama de fases Pb-Sn, movendo verticalmente na composição fornecida (em vermelho), movimentando a linha através da região α + L para a composição especificada, a temperatura é de aproximadamente 295 ° C (linha verde).

    2. Passo 2

  2. A 250 ° C e na região da fase α + L

Ca = 14% Sn-86% Pb

CL = 34% Sn-66% Pb

C0= 0,5

Então, podemos calcular através da regra da alavanca:

W α = 0,5 = C L   -   C 0 C L   -   C α

W α = 0,5 = 34   -   C o 34 -   14

Para acharmos Co basta isola-lo:

C o = 34 - ( 0,5 × 20 )

C o = 24 %   S n

Agora, massa de 24% Sn adicionada à liga para alcançar essa nova composição. A quantidade de Sn na liga original é de:

0,10 × 1,5 = 0,15   k g

Em seguida, usando uma fórmula temos:

0,15   k g   +   m S n 1,5   k g +   m S n × 100 = 24

Agora precisamos isolar m S n

0,15   k g   +   m S n × 100 = 24 × ( 1,5   k g +   m S n )  

15   k g   + 100   m S n = 36   k g +   24 m S n  

  - 24 m S n     + 100   m S n = 36   k g - 15   k g  

m S n = 0,276   k g

Resposta

  1. 295°C
  2. m S n = 0,276   k g
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cite as fases presentes e as composições das fases para as seguintes ligas:(a) 90 % p Zn- 10 % p Cu a 400 ° C( 750 ° F ) (b) 75 % p Sn- 25 % p Pb a 175 ° C( 345 ° F ) (c) 55 % p Ag- 45 % p Cu a 900 °
É possível existir uma liga de cobre-zinco que, em equilíbrio, consista em uma fase ε da composição 80%p Zn-20% p Cu, e também em uma fase líquida da composição em 95%p Zn-5% p Cu? Se isso for possíve
Desenvolva as Equações 9.6a e 9.7a, que podem ser usadas para converter fração mássica em fração volumétrica e vice-versa.
Determine as quantidades relativas (em termos de frações volumétricas) das fases para as ligas e temperaturas dadas no Problema 9.8a, b e c. A seguinte tabela fornece as massa específicas aproximadas
Determine as quantidades relativas (em termos de frações de mássicas) das fases para as ligas e temperaturas dadas no Problema 9.8.