Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 9.Perguntas e Problemas - Ex. 24

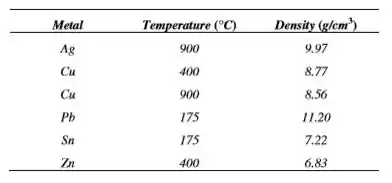
Determine as quantidades relativas (em termos de frações volumétricas) das fases para as ligas e temperaturas dadas no Problema 9.8a, b e c. A seguinte tabela fornece as massa específicas aproximadas para os vários metais nas temperaturas das ligas:

Passo 1

Para nos desenvolvermos vamos definir a equação para este propósito, que é esta a abaixo:

  1. Para a liga liga Cu-Zn a 400 ° C, tem-se os seguintes dados:

    2. Cε = 87 % Zn-13 % Cu

    Cη = 97% Zn-3% Cu

    Wε = 0,7

    Wη = 0,3

    ρCu = 8,77 g/cm³

    ρZn = 6,83 g/cm³

    Agora genteee, temos que calcular as densidades das fases ε e η aplicando a seguinte equação:

    ρ ε   = 100 C Z n ε ρ Z n   + C C u ε ρ C u  

    Substituindo os valores de massa específica e afins, listados acima temos:

    ρ ε   = 100 87 6,83   g / c m ³   + 13 8,77   g / c m ³ = 7 g / c m ³

    ρ   η   = 100 C Z n   η ρ Z n   + C C u   η ρ C u

    ρ   η     = 100 97 6,83   g / c m ³   + 3 8,77   g / c m ³ = 6,9   g / c m ³

    Agora podemos determinar os valores de Vε e Vη:

    V ε   = W ε   / ρ ε W ε       ρ ε   + W η   ρ η

    V ε   = 0,7   / 7   g / c m ³ 0,7   7   g / c m ³   + 0,3   6,9   g / c m ³ = 0,7

    V η   = W η   / ρ η W ε       ρ ε   + W η   ρ η

    V   η     = 0,3   / 6,9   g / c m ³ 0,7   7   g / c m ³   + 0,3   6,9   g / c m ³ = 0,3

    Passo 2

  2. Pb-Sn a temperatura 175°C temos os seguintes dados:

    3. Cα = 16% Sn-84 % Pb

    Cβ = 97 % Sn-3 t% Pb

    Wα = 0,27

    Wβ = 0,73

    ρSn = 7,22 g/cm³

    ρPb = 11,20 g/cm³

    Agora genteee, temos que calcular as densidades das fases α e β aplicando a seguinte equação:

    ρ α   = 100 C S n α ρ S n   + C P b α ρ P b  

    Substituindo os valores de massa específica e afins, listados acima temos:

    ρ α   = 100 16 7,22   g / c m ³   + 84 11,2   g / c m ³ = 10,3   g / c m ³

    ρ β   = 100 C S n β ρ S n   + C P b β ρ P b  

    ρ β   = 100 97 7,22   g / c m ³   + 3 11,2   g / c m ³ = 7,3   g / c m ³

    Agora podemos determinar os valores de V α e V β :

    V α   = W α   / ρ α W α       ρ α   + W β   ρ β

    V α   = 0,27   / 10,3   g / c m ³ 0,27   10,3   g / c m ³   + 0,73   7,3   g / c m ³ = 0,21

    V β   = W β   / ρ β W α       ρ α   + W β   ρ β

    V β   = 0,73   / 7,3   g / c m ³ 0,27   10,3   g / c m ³   + 0,73   7,3   g / c m ³ = 0,79

    Passo 3

  3. Ag-Cu a 900 ° C, apresenta apenas fase líquida. Assim sendo, VL = 1,0

Resposta

  1. ρ ε   = 7 g c m 3 ;   ρ   η = 6,9 g c m 3 ;   V ε   = 0,7 ;   V   η   = 0,3
  2. ρ α   = 10,3 g c m 3 ;   ρ β   = 7,3 g c m 3 ;   V α   = 0,21 ;   V β   = 0,79
  3. VL = 1,0
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma liga contendo 30%p Sn-70% p Pb é aquecida até uma temperatura na região das fases β + líquido Se a fração mássica de cada fase é de 0,5, estime: a) A temperatura da ligab) As composições das duas
Uma liga de 90% p Ag-10% p Cu é aquecida até uma temperatura na região das fases β + líquido. Se a composição da fase líquida for 85%p Ag, Determine: a) A temperatura da liga b) A composição da fase β
Para ligas de dois metais hipotéticos A e B, existe uma fase α rica em A, e uma fase β, rica em B. A partir das frações mássicas de ambas as fases para duas ligas diferentes dadas na tabela a seguir (
Uma liga hipotética A-B com composição 55% B -45% A, em uma dada temperatura, consiste em frações mássicas de 0,5 para ambas as fases α e β. Se a composição da fase β é de 90%B-10% A, qual é a composi
É possível haver uma liga de cobre-prata com composição 50% Ag-50% Cu, a qual, em equilíbrio, consiste nas fases α e β com frações mássicas de W α = 0,60 e W β = 0,40? Se isso for possível, qual será