Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 8.Perguntas e Problemas - Ex. 16
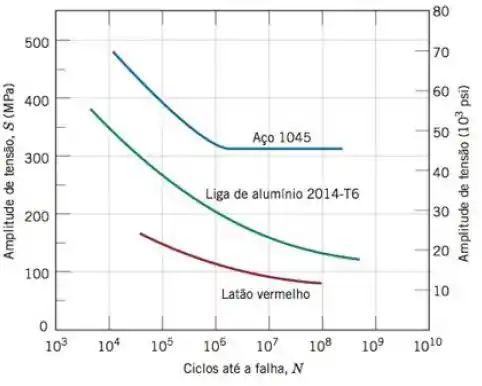
Uma barra cilíndrica com 8,0mm (0,31in) de diâmetro, fabricada a partir de uma liga de latão vermelho (Figura 8.34), é submetida a um ciclo de aplicação de cargas alternadas de tração e de compressão ao longo do seu eixo. Se as cargas de tração e de compressão máximas são de +7500N (+1700) e -7500N (-1700), respectivamente, determine sua vida em fadiga. Assuma que a tensão traçada na Figura 8,34 seja a amplitude de tensão.
Passo 1
Somos solicitados a determinar a vida em fadiga de uma barra de latão vermelha cilíndrica, considerando seu diâmetro (8,0 mm) e as cargas máximas de tração e compressão (+7500 N e -7500 N, respectivamente). A primeira coisa que é necessária é calcular os valores de e usando a Equação 6.1. Portanto:
Passo 2
Agora torna-se necessário calcular a amplitude de tensão usando a Equação 8.16:
Na Figura 8.34, f para o latão vermelho, o número de ciclos até a falha nessa amplitude de tensão é de cerca de
Abaixo a figura 8.34:
